Solve for matrix X: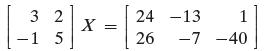

Use the following discussion for Problems 94 and 95. In graph theory, an adjacency matrix, A, is a way of representing which nodes (or vertices) are connected. For a simple directed graph, each entry, aij , is either 1 (if a direct path exists from node i to node j) or 0 (if no direct path exists from node i to node j). For example, consider the following graph and corresponding adjacency matrix.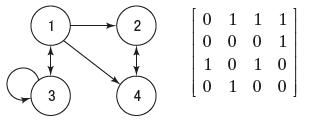

The entry a₁₄ is 1 because a direct path exists from node 1 to node 4. However, the entry a41 is 0 because no path exists from node 4 to node 1. The entry a33 is 1 because a direct path exists from node 3 to itself. The matrix Bk = A + A² + . . . + A^k indicates the number of ways to get from node i to node j within k moves (steps).

32 -1 5 X 1 -7 -40 24 -13 26