Suppose that the scalar function u(t) and the vector function r(t) are both defined for a ≤ t ≤ b.

a. Show that ur is continuous on [a, b] if u and r are continuous on [a, b].

b. If u and r are both differentiable on [a, b], show that ur is differentiable on [a, b] and that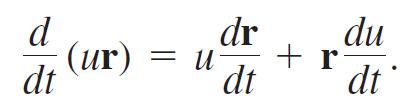

d dt (ur) = dr dt + r du dt