Suppose that the temperature in a long, thin rod placed along the x-axis is initially C/(2a) if
Question:
Suppose that the temperature in a long, thin rod placed along the x-axis is initially C/(2a) if |x | < a and 0 if |x | > a. It can be shown that if the heat diffusivity of the rod is k, then the temperature of the rod at the point x at time t is
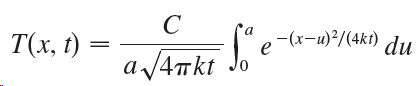
To find the temperature distribution that results from an initial hot spot concentrated at the origin, we need to compute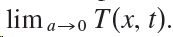 
Use l’Hospital’s Rule to find this limit.
The word "distribution" has several meanings in the financial world, most of them pertaining to the payment of assets from a fund, account, or individual security to an investor or beneficiary. Retirement account distributions are among the most...
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Both numerator and denominator approach 0 as a 0 so ...View the full answer
Answered By
Tobias sifuna
I am an individual who possesses a unique set of skills and qualities that make me well-suited for content and academic writing. I have a strong writing ability, allowing me to communicate ideas and arguments in a clear, concise, and effective manner. My writing is backed by extensive research skills, enabling me to gather information from credible sources to support my arguments. I also have critical thinking skills, which allow me to analyze information, draw informed conclusions, and present my arguments in a logical and convincing manner. Additionally, I have an eye for detail and the ability to carefully proofread my work, ensuring that it is free of errors and that all sources are properly cited. Time management skills are another key strength that allow me to meet deadlines and prioritize tasks effectively. Communication skills, including the ability to collaborate with others, including editors, peer reviewers, and subject matter experts, are also important qualities that I have. I am also adaptable, capable of writing on a variety of topics and adjusting my writing style and tone to meet the needs of different audiences and projects. Lastly, I am driven by a passion for writing, which continually drives me to improve my skills and produce high-quality work.
1+ Reviews
10+ Question Solved
Related Book For 
Question Posted:
