Suppose that (x) is differentiable on an interval centered at x = a and that g(x) = b 0 + b 1 (x - a)

Suppose that ƒ(x) is differentiable on an interval centered at x = a and that g(x) = b₀ + b₁(x - a) + · · · + b_n(x - a)ⁿ is a polynomial of degree n with constant coefficients b₀, . . . , b_n. Let E(x) = ƒ(x) - g(x). Show that if we impose on g the conditions.

i) E(a) = 0

ii)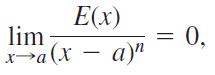

then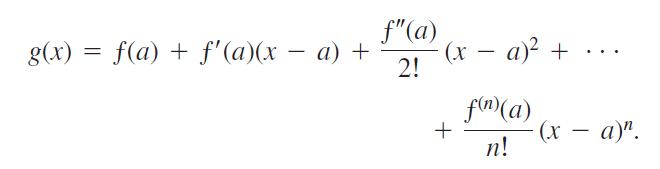

Thus, the Taylor polynomial P_n(x) is the only polynomial of degree less than or equal to n whose error is both zero at x = a and negligible when compared with (x - a)ⁿ.

E(x) lim xa(x-a)n 0,