The accompanying figure shows a typical point P(x₀, y₀) on the parabola y² = 4px. The line L is tangent to the parabola at P. The parabola’s focus lies at F( p, 0). The ray L′ extending from P to the right is parallel to the x-axis. We show that light from F to P will be reflected out along L′ by showing that β equals α. Establish this equality by taking the following steps.

a. Show that tan β = 2p/y₀.

b. Show that tan ϕ = y₀/(x₀ - p).

c. Use the identity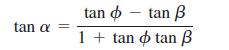

to show that tan a = 2p/y₀.

Since a and b are both acute, tan β = tan a implies β = α.

This reflective property of parabolas is used in applications like car headlights, radio telescopes, and satellite TV dishes.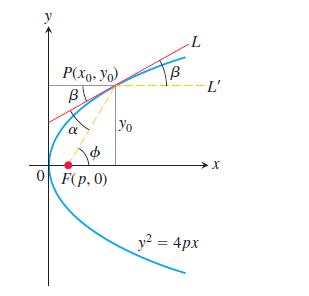

tan a = tantan B 1 + tan tan B