The direction angles , , and of a vector v = ai + bj + ck are defined as follows: is the angle

The direction angles α, β, and γ of a vector v = ai + bj + ck are defined as follows:

α is the angle between v and the positive x-axis (0 ≤ α ≤ π)

β is the angle between v and the positive y-axis (0 ≤ β ≤ π)

γ is the angle between v and the positive z-axis (0 ≤ γ ≤ π).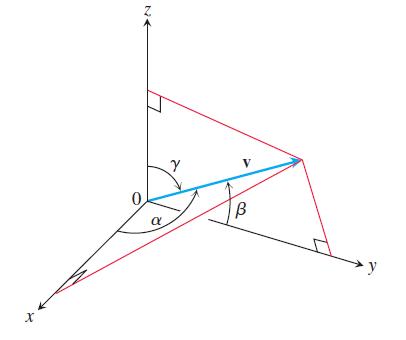

a. Show that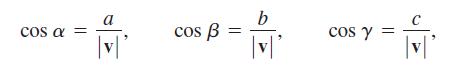

and cos²α + cos²β + cos²γ = 1. These cosines are called the direction cosines of v.

b. Unit vectors are built from direction cosines Show that if v = ai + bj + ck is a unit vector, then a, b, and c are the direction cosines of v.

X 0 Y V B