Question: The equation ax 2 + 2x - 1 = 0, where a is a constant, has two roots if a > -1 and a

The equation ax² + 2x - 1 = 0, where a is a constant, has two roots if a > -1 and a ≠ 0, one positive and one negative: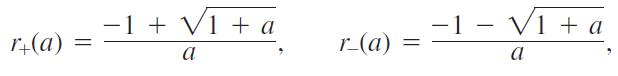 a D + IA - I- = (1)-1 a D + IA

a. What happens to r+(a) as a→ 0? As a→ -1⁺?

b. What happens to r-(a) as a→ 0? As a→ -1⁺?

c. Support your conclusions by graphing r₊(a) and r_-(a) as functions of a. Describe what you see.

d. For added support, graph ƒ(x) = ax² + 2x - 1 simultaneously for a = 1, 0.5, 0.2, 0.1, and 0.05.

a D + IA - I- = (1)-1 a D + IA + I- = r+(a)

Step by Step Solution

★★★★★

3.43 Rating (169 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a To find what happens to ra as a approaches 0 and as a approaches 1 from the right we can use limit... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

The following additional information is available for the Dr. Ivan and Irene Incisor family from Chapters 1-5. Ivan's grandfather died and left a portfolio of municipal bonds. In 2012, they pay Ivan...

If a single constant force acts on an object that moves on a straight line, the objects velocity is a linear function of time. The equation v = vi + at gives its velocity v as a function of time,...

The figure shows a fixed circle C1 with equation (x 1)2 + y2 = 1 and a shrinking circle C2 with radius and center the origin. P is the point (0, r), Q is the upper point of intersection of the two...

In python: I have this so far but not sure how to get it to work or incorporate the positive and negative equation to it. def positive(value): if value > 0: return value if value

THIS IS USING C++ Pay special attention to the style of your code. Indent your code correctly, choose meaningful names for your variables, define constants where needed, choose most suitable control...

CPE 2073 Homework 6 Objective Practice if...else statements. Background In homework assignments we evaluated quadratic equations, that is, we calculated y = ax? + bx + c. for given values of x, a, b,...

a. -5 and - 8 c. -5 and 8 Instructions. Write ABCD if the equation shown is a quadratic equation, WXYZ if the equation shown is not a quadratic equation. b. 5 and - 8 d. 5 and 8 1, 3x + 36 6 15x +...

In Example 5, change the + sign before the 5x to . Data from Example 5 Find the roots of the equation 2x 3 + x 2 + 5x 3 = 0. Because n = 3, there are three roots. If we can find one of these roots,...

Question: 2. Consider a particle in an infinite square well. It is in the initial state y(x, 0) = A [$1(x) + $2(x)] where on (x) is the energy eigenfunctions for the infinite square well. (a) Plot...

Help me complete exercises 10, 12, 14, 18, 20, 22 please. EXERCISES Practice List the possible rational roots of each equation. Then determine the rational roots. 10. x3 + 2x2 - 5x - 6 = 0 11. x3 -...

Fill in the missing annual interest rates in the following table for an ordinary annuitystream. Number of Payments or Years 10 20 30 100 Annual Interest Rate Future Value Anuity Present Value...

Let H be a separable Hilbert space, and (e,) C Ha total orthonormal sequence in H. Let T: H H be the right shift operator, defined as Tx = (x, en-1)en for every x = >(x, en)en- n=2 n=1 Note that, in...

The objective of trading Long - The - Basis is to: generate margins by capturing a rise in basis. generate margins by capturing a fall in basis. generate margins through cash price changes. generate...

Shard Crockery Co. recognized the following events related to customer accounts receivable during 2000.At the start of the year,the firm reported gross accounts receivable of $22,000,000 and an...

In problem, use the given function f to: (a) Find the domain of f. (b) Graph f. (c) From the graph, determine the range and any asymptotes of f. (d) Find f -1 , the inverse of f. (e) Find the domain...

In problem, the function f is one-to-one. Find its inverse and check your answer. Graph f, f -1 , and y = x on the same coordinate axes. f(x) = 1/x - 2

If the amount that $1000 will purchase is only $950 after 2 years, what was the average inflation rate? Inflation problem require the following discussion. Inflation is a term used to describe the...

As the maturity of bonds approaches, premium bond prices approach. and discount bond prices approach. assuming the bond issuer and other market conditions stay the same. zero; par value discount...

Exercise 6-10 Suppose this information is available for PepsiCo, Inc. for 2012, 2013, and 2014. See image below: Please find the following: 1. Calculate the inventory turnover for PepsiCo., Inc. for...

You are thinking of building a new machine that will save your company $1,000 in the first year. The machine will then begin to wear out so that the savings decline at a rate of 2% per year forever....