The graph of a function consists of a semicircle and two line segments as shown. Let
Question:
The graph of a function ƒ consists of a semicircle and two line segments as shown. Let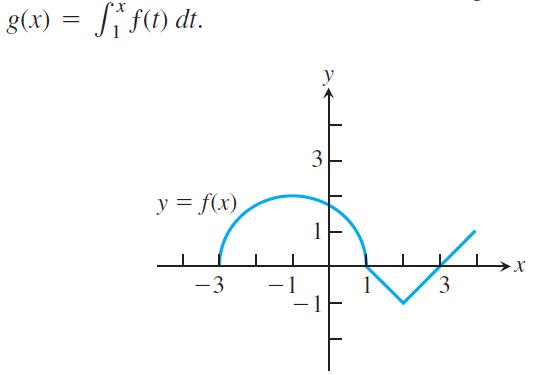
a. Find g(1).
b. Find g(3).
c. Find g(-1).
d. Find all values of x on the open interval (-3, 4) at which g has a relative maximum.
e. Write an equation for the line tangent to the graph of g at x = -1.
f. Find the x-coordinate of each point of inflection of the graph of g on the open interval (-3, 4).
g. Find the range of g.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
To solve these questions lets first analyze the given function and then proceed with the calculations The graph of consists of a semicircle with coord...View the full answer
Answered By
User l_917591
As a Business Management graduate from Moi University, I had the opportunity to work as a tutor for undergraduate students in the same field. This experience allowed me to apply the theoretical knowledge I had gained in a practical setting, while also honing my teaching and communication skills.
As a tutor, I was responsible for conducting tutorial sessions, grading assignments and exams, and providing feedback and support to my students. I also assisted with the preparation of course materials and collaborated with other tutors and professors to ensure consistency in teaching and assessment.
0 Reviews
10+ Question Solved
Related Book For 
Thomas Calculus Early Transcendentals
ISBN: 9780321884077
13th Edition
Authors: Joel R Hass, Christopher E Heil, Maurice D Weir
Question Posted:
