Question: The tangent line to a circle may be defined as the line that intersects the circle in a single point, called the point of tangency.

The tangent line to a circle may be defined as the line that intersects the circle in a single point, called the point of tangency. See the figure.

Уд


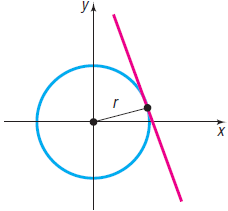
If the equation of the circle is and the equation of the tangent line is, show that:

If the equation of the circle is x2 + y2 = r2 and the equation of the tangent line is y = mx + b, show that:

(a) r2 (1 + m2) = b2

The quadratic equation x2 + (mx + b) 2 = r2 has exactly one solution.

(b) The point of tangency is (-r2m/b, r2/b).

(c) The tangent line is perpendicular to the line containing the center of the circle and the point of tangency.

Step by Step Solution

★★★★★

3.57 Rating (157 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

a There is one solution if and only if the discriminant is zero b Using the quadratic ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

Q:

Refer to Problem 52.The line x 2y + 4 = 0 is tangent to a circle at (0, 2).The line y = 2x 7 is tangent to the same circle at (3, -1). Find the center of the circle. Data from problem 52 The tangent...

Q:

The Greek method for finding the equation of the tangent line to a circle uses the fact that at any point on a circle the lines containing the center and the tangent line are perpendicular (see...

Q:

Use the Greek method described in Problem 53 to find an equation of the tangent line to the circle x2 + y2 4x + 6y + 4 = 0 at the point (3, 22 - 3). Data form problem 53 The Greek method for finding...

Q:

The tangent line to a circle may be defined as the line that intersects the circle in a single point called the point of tangency Find the standard form of the equation of the circle with center 9 6...

Q:

I need help with this big problem 1-6 . Could you explain step by step for these questions please and thank you . D =90 Jerry 2022 Home Zoom Announcements Modules Syllabus Discussions Grades NetTutor...

Q:

Main Ideas/Questions Notes/Examples Tangent A tangent line intersects a circle at exactly point, called the point of tangency. LINES A line is tangent to a circle if and only if it is to a drawn to...

Q:

A line segment that intersects the circle at one point. Question 4 (0.5 points) Listen Which of the following statements defines a tangent line to a circle? A line that intersects a circle in two...

Q:

please break down the process and provide the name of the rules. Compare the following two equations describing familiar curves: y =x +3 (parabola) and x +y =4 (circle). The first equation defines y...

Q:

Let P(5, 12) be a point on the circle x 2 + y 2 = 169 (see figure). (a) What is the slope of the line joining P and O(0, 0)? (b) Find an equation of the tangent line to the circle at P. (c) Let Q(x,...

Q:

Let P(3, 4) be a point on the circle x2 + y2 = 25 (see figure). (a) What is the slope of the line joining P and O(0, 0)? (b) Find an equation of the tangent line to the circle at P. (c) Let Q(x, y)...

Q:

Write the equation for the node-1 (number( 2 3 Ohm 7 Ohm 5 A 8 Ohm 1A a) V2 =(1/82 +1/30) V2 - (1/30) V1 =5 A O b) V2 =(1/8Q +1/32) V2 + (1/32) V1 =5 A O c) V2 =(1/3N +1/30) V2 + (1/8N) V =5 A d) V2...

Q:

According to the semi-strong form of the efficient market hypothesis, which of the following might lead to extraordinary profits? A. studying charts of a stock's past price behavior B. thoroughly...

Q:

The Black Star fund has assets with a market value of 1 2 . 6 million and liabilities of 8 0 0 , 0 0 0 . What is the net asset value if there are 2 0 0 , 0 0 0 shares outstanding

Q:

14-7. You are ready to finally plan your family summer vacation. After what seems like an eternity of long hours at work, you deserve a week of total relaxation. Now, where do you go? The mountains?...

Q:

Benjamin owns a small Internet business. Besides himself, he employs nine other people. The salaries earned by the employees are given next in thousands of dollars (Benjamins salary is the largest,...

Q:

Benjamin owns a small Internet business. Besides himself, he employs nine other people. The salaries earned by the employees are given next in thousands of dollars (Benjamins salary is the largest,...

Q:

Each of the following three data sets represents the IQ scores of a random sample of adults. IQ scores are known to have a mean and median of 100. For each data set, determine the sample standard...

Q:

What is the annual rate of return on the stock (percentage) before tax? A. 37.67% B. 23.55% C. 29.19% D.18.45% E. 21.80% Please I need help with the solution and steps to get to the solution. Thank...

Q:

Muscarella Inc. has the following balance sheet and income statement data: Cash $ 14,000 Accounts payable $ 42,000 Receivables 70,000 Other current liabilities 28,000 Inventories 210,000 Total CL $...

Q:

The Biltmore Equipment Co. just issued 250,000 zero coupon bonds. These bonds. mature in 30 years, have a par value of $1,000, and have a yield to maturity of 7.25 percent. WHat is the approximate...