Use the Intermediate Value Theorem from Section 2.5 to show that (x) = x 3 + 2x - 4 has a root between x =

Use the Intermediate Value Theorem from Section 2.5 to show that ƒ(x) = x³ + 2x - 4 has a root between x = 1 and x = 2. Then find the root to five decimal places.

Intermediate Value Theorem from Section 2.5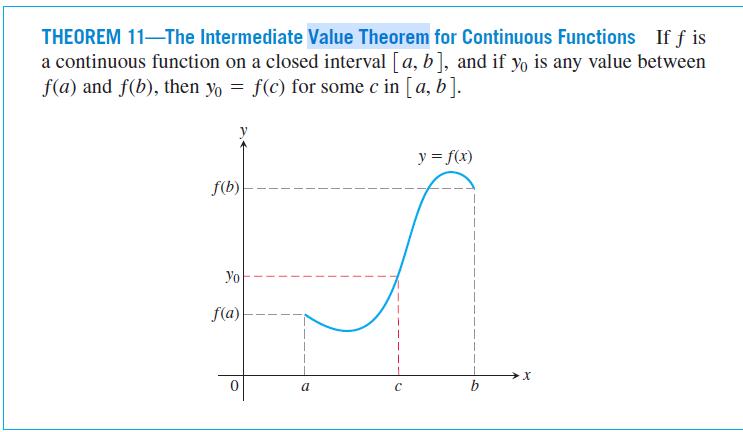

THEOREM 11-The Intermediate Value Theorem for Continuous Functions If f is a continuous function on a closed interval [a, b], and if yo is any value between f(a) and f(b), then yo = f(c) for some c in [a, b]. f(b) Yo f(a) a C y = f(x) X