Assume that a data stream d(t) consists of a random (coin-toss) sequence of + 1s and -1s each of which is T seconds in duration. The auto correlation function for such a sequence is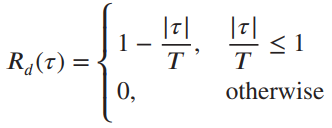 

(a) Find and sketch the power spectral density for an ASK-modulated signal given by 

where θ is a uniform random variable in (0, 2π].

(b) Use the result of Problem 9.21(a) to compute and sketch the power spectral density of a PSK-modulated signal given by 

for the three cases m = 0,0.5, and 1.

|| R4(t) 0, otherwise SASK (1) = A[1+d (t)] cos(@t + 0) A [1+d (t)]cos(@t +0)