It can be shown that a necessary and sufficient condition for the existence of an instantaneous binary code with word lengths I_i, 1 ‰¤ i ‰¤ N, is 

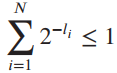
This is known as the Kraft inequality. Show that the Kraft inequality is satisfied by the code words given in Table 12.3. (Note: The inequality given above must also be satisfied for uniquely decipherable codes.)

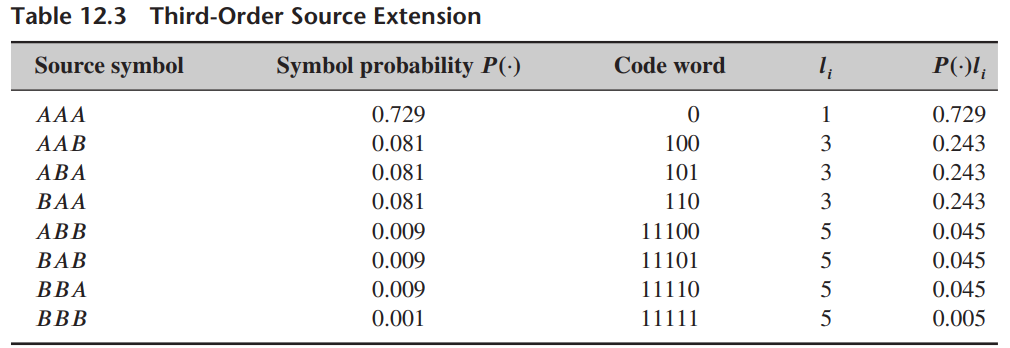
2-li < 1 i=1 Table 12.3 Third-Order Source Extension Source symbol Symbol probability P() Code word P(:), AAA 0.729 1 0.729 AAB 0.081 100 0.243 0.081 0.081 ABA 101 3 0.243 BAA 110 3 0.243 11100 11101 ABB 0.009 5 0.045 BAB 0.009 5 0.045 BBA 0.009 0.001 11110 0.045 BBB 11111 5 0.005