2.5. A Markov chain has the transition probability matrix

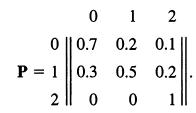
The Markov chain starts at time zero in state X0 = 0. Let T=min{n? 0; X,, =2}
be the first time that the process reaches state 2. Eventually, the process will reach and be absorbed into state 2. If in some experiment we observed such a process and noted that absorption had not yet taken place, we might be interested in the conditional probability that the process is in state 0 (or 1), given that absorption had not yet taken place. Determine Pr(X3=OJX0,T>3).
Hint: The event IT > 3) is exactly the same as the event {)(0 2) = {X3 = 0) U {X3 = I).

1 2 01 0 || 0.7 0.2 0.1 P 10.3 0.5 0.2 2 0 0 1