31. Let N(t), t 0 be a Poisson process with rate . Suppose that N(t) is the total number of two types of events

31. Let

N(t), t ≥ 0

be a Poisson process with rate λ. Suppose that N(t) is the total number of two types of events that have occurred in [0, t]. Let N1(t) and N2(t) be the total number of events of type 1 and events of type 2 that have occurred in [0, t], respectively. If events of type 1 and type 2 occur independently with probabilities p and 1 − p, respectively, prove that

N1(t), t ≥ 0

and

N2(t), t ≥ 0

are Poisson processes with respective rates λp and λ(1 − p).

Hint: First calculate P

????

N1(t) = n and N2(t) = m

using the relation

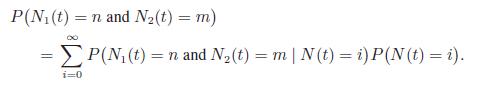
(This is true because of Theorem 3.4.) Then use the relation

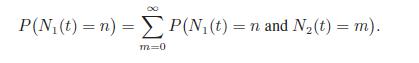
P(N(t)=n and N2(t) = m) = P(N(t) = n and N2(t) = m | N(t) = i)P(N(t) = i). i=0