35. For > 0, > 0, and > 0, the following function is called the bivariate Dirichlet probability density function if x

35. For α > 0, β > 0, and γ > 0, the following function is called the bivariate Dirichlet probability density function

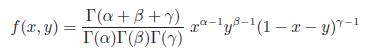
if x ≥ 0, y ≥ 0, and x + y ≤ 1; f(x, y) = 0, otherwise. Prove that fX, the marginal probability density function of X, is beta with parameters (α, β + γ); and fY is beta with the parameters (β, α + γ).
Hint: Note that

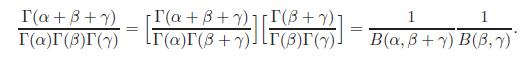
T(a+B+7) f(x, y) ra-y-(1-x-y)-1 T(a)(3)(y)