Question: n n E m Oi=1 II 1 + 0) nm i=1X1, X2, . . . ,Xn are independent random variables With the common probability density

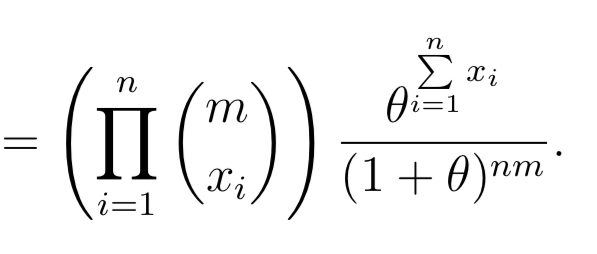
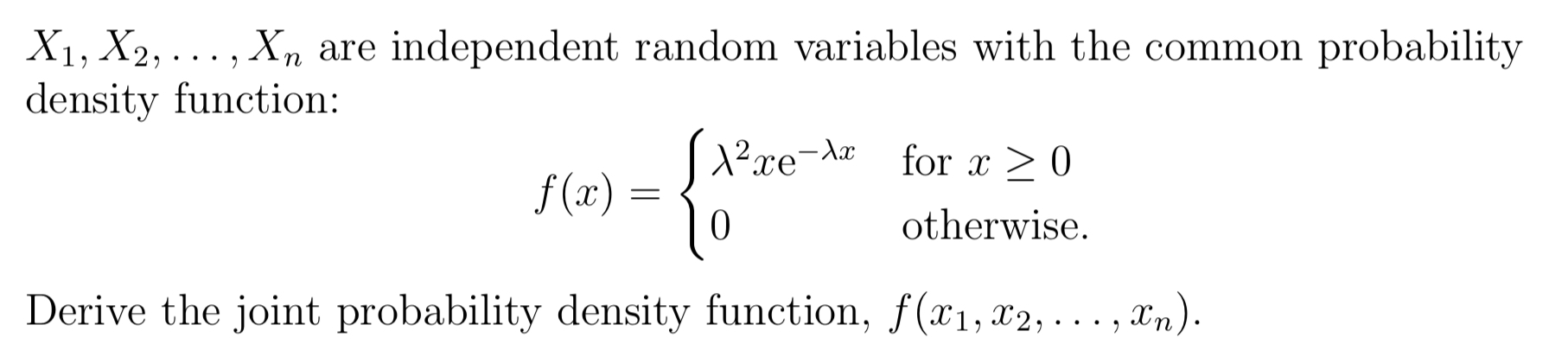
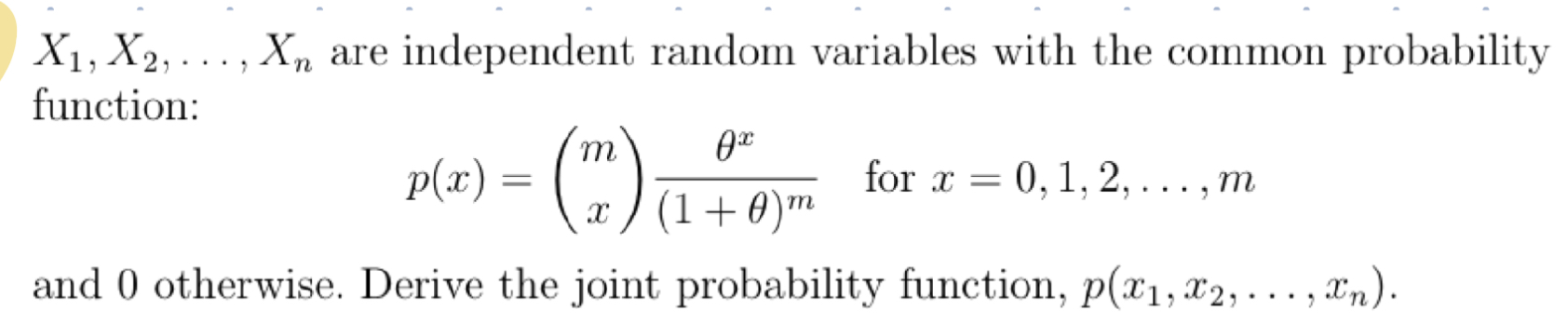
probability density function: VaseM3 for a" 2 0 m = { 0

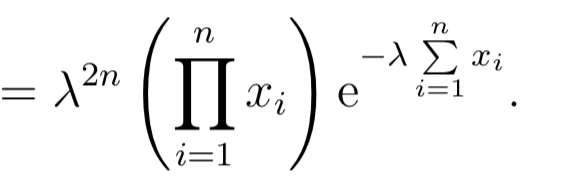
otherwise. Derive the joint probability density function, f (11:1, x2, . .

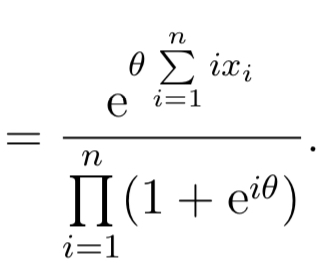
. ,xn). X 1, X 2,. . . ,X.n are independent random

$variables with the (10111111011 probability function: 711 9\": = f = .1.2,...,$

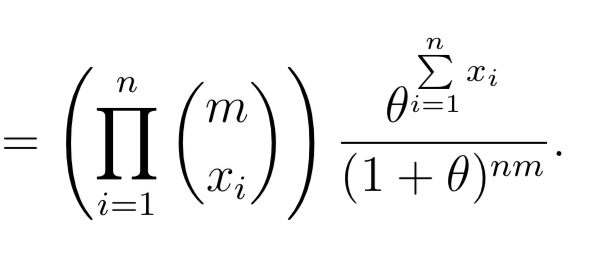
p(:1:) (3:) (1 + 9)?\" or :1: 0.4 , m and 0

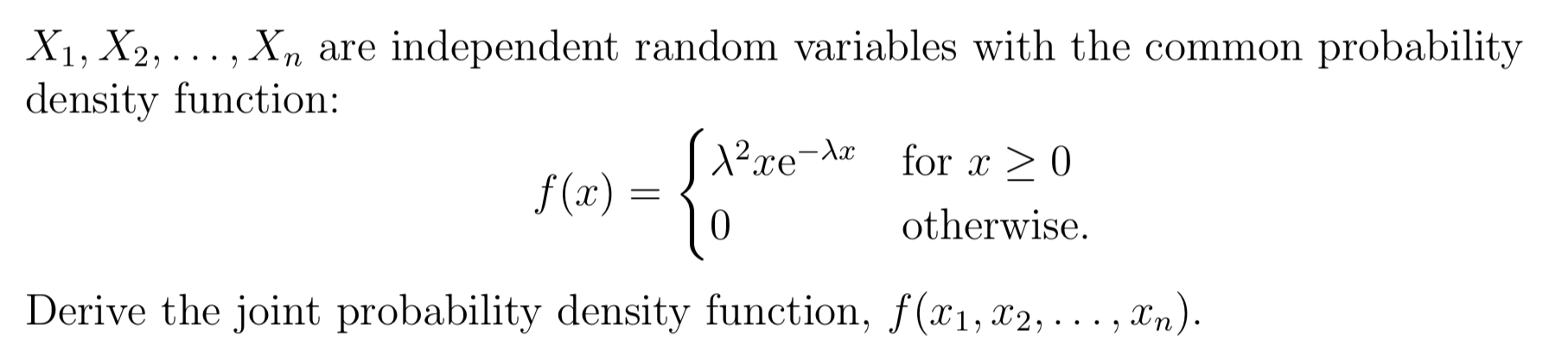
otherwise. Derive the joint probability function, p(z1,m2, . . . ,SCn). n

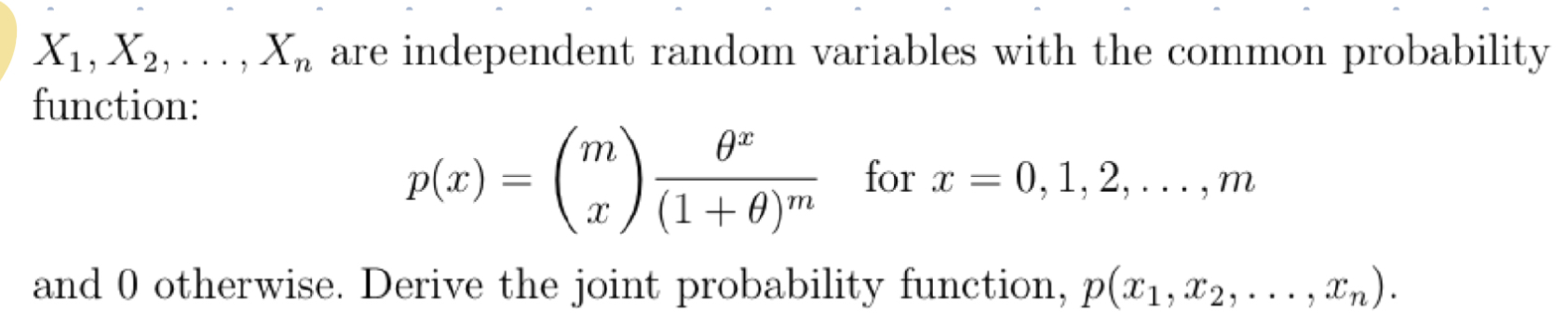
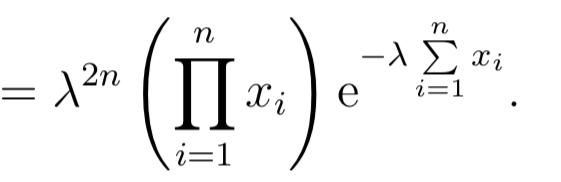
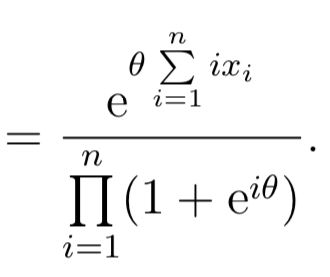
n n E m Oi=1 II 1 + 0) nm i=1X1, X2, . . . ,Xn are independent random variables With the common probability density function: VaseM3 for a" 2 0 m = { 0 otherwise. Derive the joint probability density function, f (11:1, x2, . . . ,xn). X 1, X 2,. . . ,X.n are independent random variables with the (10111111011 probability function: 711 9\": = f = .1.2,..., p(:1:) (3:) (1 + 9)?\" or :1: 0.4 , m and 0 otherwise. Derive the joint probability function, p(z1,m2, . . . ,SCn). n n 2n Exi e i=1 i=1\fX1, X2, . .., Xn are independent Bernoulli random variables. The probability function of X; is given by: (1 - 7Al-in; for xi = 0, 1 p(xi) = 0 otherwise where: Thi 1 + eie for i = 1, 2, ..., n. Derive the joint probability function, p(x1, x2, . . ., In)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Since the early 1990s, woodstove sales have declined from 1,200,000 units per year to approximately 100,000 units per year. The decline has occurred because of (1) stringent new federal EPA...

QUESTION: 1. For each elaim below, write: (1) claim in mathematical form; (2) Null hypothesis (Ho); (3) alternative hypothesis (H,); (4) what tailed test. Use notations Hi. Hz (for mean), P-Pz (for...

Let X : (X1, . . . , Xn)T be a collection of Nd. random variables with probability density function (pdf): f(.L, )w3, U is an unknown parameter. Let x : (:51, . . . , LE\")T be a random sample...

stat5102 HW5 Each problem worths 20 points. Problem 1. Let Y1 Bin(2007, p). (a) Compute the Fisher information I1 (p). (b) Let W (Y1 ) represent an unbiased estimator of p. Use the Information...

Math 180A - Homework 9 ( Due Monday Nov 28, 2:00 PM) Reading: Sections 6.1 - 6.3, 7.2 and 7.4 of the textbook. Show FULL JUSTIFICATION for all your answers. 1 Warm up Problems - Do not turn in 1....

EE 503 : HW 4 Due : 10/3/2016, Monday in class. 1. Let X1 and X2 be two random variables. Define G as G = E [max (X1 , X2 )] + E [min (X1 , X2 )] . Express G in terms of E[X1 ] and E[X2 ]. 2. A point...

1. For each Claim below, write: (1) claim in mathematical form; (2) Null hypothesis (Ho); (3) alternative hypothesis (H,); (4) what tailed test. Use notations Hi. Hz (for mean), P-Pz (for...

Help needed: 2. Consider an experiment of mating rabbits. We watch the evolution of a particularIn the Dark Ages, Harvard, Dartmouth, and Yale admitted only male students. As- sume that, at that...

HElp needed 2. Consider an experiment of mating rabbits. We watch the evolution of a particularIn the Dark Ages, Harvard, Dartmouth, and Yale admitted only male students. As- sume that, at that time,...

please answer question Answer each of the questions in the space below. {Total mark: 2?]; 2 marks for each question] 1. Suppose X 2 Bin{n, p} with n = 15 and p = {1.4, Y N Poissonlipt} with p, = 21 X...

Let X1, X2, ., X, be independent continuous random variables with common density function f Let X,, denote the ith smallest of X, .., X. (a) Note that in order for X,, to equal x, exactly i - 1 of...

What are Pr and vr called? Is their use limited to isentropic processes? Explain.

United States Motors Inc. (USMI) manufactures automobiles and light trucks and distributes them for sale to consumers through franchised retail outlets. As part of the franchise agreement,...

Marty, a 1 6 - year - old, contracted with Cream - of - the - Crop Cycles to buy an $ 8 , 0 0 0 motoreycle. He agreed to make moethly payments until the purchase price plas interest were paid in...

Find the exact value of each expression. a. b. c. d. -14 sin sin sin(sn(-3) sin sin cos (cos (-45))

Several technologies have been practically given away by the United States to the world. Name at least two such technologies. Do you think that this was charity or that the United States reaps some...

What are the elements that make the responsibilities of IT professionals similar to those of other professionals, such as engineers and financial analysts?

IBM Credit was a wholly owned subsidiary of IBM responsible for financing mainframe computers sold by IBM. While some customers bought mainframes outright or obtained financing from other sources,...

Country A and country B both have the production function Y = F(K, L) = K1/2L1/2. a. Does this production function have constant returns to scale? Explain. b. What is the per-worker production...

REVIEW THE INFORMATION ABOUT LEAPFROG HOSPITAL SAFETY GRADES. CHOOSE TWO HOSPITALS TO COMPARE A VERY EFFECTIVE ONE AND ONE WHICH IS NOT EFFECTIVE. WHAT SEPARATES THE TWO? HOW CAN THE A HOSPITAL USE...

2. To understand that as a general rule it takes about 3 minutes before the other part(s) have made up a 90% impression of you.

3. To understand that the first impression means a lot, and it takes a lot of energy to change this first impression.

Go, do not wait until I come