4.11. Computer Challenge Let U0, U,, . . . be independent random variables, each uniformly distributed on the interval (0, 1). Define a stochastic process {S,,} recursively by setting

(This is an example of a discrete-time, continuous-state, Markov process.)
When n becomes large, the distribution of S,, approaches that of a random variable S = SF, and S must have the same probability distribution as U(1 + S), where U and S are independent. We write this in the form 2b S = U(1 + S), from which it is easy to determine that E[S] = 1, Var[S] and even (the Laplace transform)

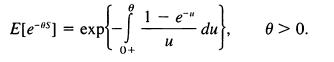
The probability density functionf(s) satisfies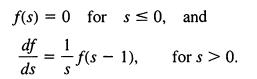

What is the 99th percentile of the distribution of S? (Note: Consider the shot noise process of Section 4.1. When the Poisson process has rate A = I and the impulse response function is the exponential h(x) = exp{-x}, then the shot noise 1(t) has, in the limit for large t, the same distribution as S.)

S =0 and S+1 = =U,,(1 + S) for n > 0.