9. Let X be a continuous random variable with probability density function f.We say that X is symmetric about if for all x,

(a) Prove that X is symmetric about α if and only if for all x, we have f(α − x) = f(α + x).

(b) Show that X is symmetric about α if and only if f(x) = f(2α − x) for all x.

(c) Let X be a continuous random variable with probability density function

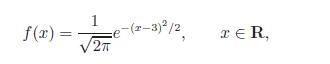
and Y be a continuous random variable with probability density function

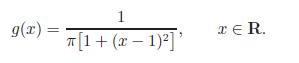
Find the points about which X and Y are symmetric.

P(Xa+x) = P(X a-x).