A modulated signal (pulse code modulation) \(\{X(t), t \in(-\infty,+\infty)\}\) is given by

\[X(t)=\Sigma_{-\infty}^{+\infty} A_{n} h(t-n)\]

where the \(A_{n}\) are independent and identically distributed random variables which can only take on values -1 and +1 and have mean value 0 . Further, let

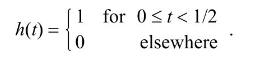
(1) Sketch a possible sample path of the stochastic process \(\{X(t), t \in(-\infty,+\infty)\}\).
(2) Determine the covariance function of this process.
(3) Let \(Y(t)=X(t-Z)\), where the random variable \(\mathrm{Z}\) has a uniform distribution over \([0,1]\).
Is \(\{Y(t), t \in(-\infty,+\infty)\}\) a weakly stationary process?

1 for 0