Let the interarrival times i have a geometric distribution; namely, P( i = m) = p(1 p) m1 for m = 1,2, ... and

Let the interarrival times τ_i have a geometric distribution; namely, P(τ_i = m) = p(1− p)^m−1 for m = 1,2, ... and a parameter p ∈ (0,1).

(a) Show that T_n has a negative binomial distribution. With which parameters?

(b) Show that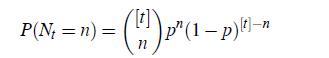

for n ≤ [t], where [t] stands for the integer part of t.

(c) Is the process N_t that with independent increments?