Question: Let X 1 ,X 2 , ... be a sequence of independent r.v.s uniformly distributed on the interval [0,2], and let S n = X

Let X1,X2, ... be a sequence of independent r.v.’s uniformly distributed on the interval [0,2], and let Sn = X1 + ... + Xn.

(a) Find E{Sn} and Var{Sn}.

(b) Using the Central Limit Theorem, estimate P(n − √n ≤ Sn ≤ n + √n).

(c) Write down a formula for the limit of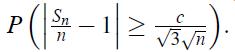Let X1,X2, ... be a sequence of independent r.v.’s uniformly distributed on

Proceeding from the formula you have obtained, explain why the accuracy with which the average X̅n = Sn is close to 1 has an order of 1/√n.

Step by Step Solution

★★★★★

3.44 Rating (157 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

a Since EX 1 and VarX 2 1 we have ES n and Var Sn b Pn ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Probability And Stochastic Modeling Questions!

Q:

Let X1, X2, , Xn be uniformly distributed on the interval 0 to a. Recall that the maximum likelihood estimator of a is a = max (Xi). (a) Argue intuitively why cannot be an unbiased estimator for a....

Q:

Let X 1 , X 2 , ¦ , X n be uniformly distributed on the interval 0 to a. Recall that the maximum likelihood estimator of a is aÌ = max(X i ). (a) Argue intuitively why Ëa cannot be...

Q:

Let X1, X2, , Xn be uniformly distributed on the interval 0 to a. Show that the moment estimator of a is a = aX. Is this an unbiased estimator? Discuss the reasonableness of this estimator.

Q:

Generalizing Exercise 5-c for r.v.s X i having a mean of m and a variance of 2 , find the limit Comment on your result and connect it with the LLN. Exercise 5-c Let X 1 ,X 2 , ... be a sequence of...

Q:

Let X = max{U1,U2, . . . ,UN }, where the Ui are independent random variables uniformly distributed on (0, 1) and N is an independent random variable whose distribution is given by P(N = k) = 1 (e ...

Q:

Given: . Probability Density Function (PDF): 0(1 -2)0-1 if0 0 is an unknown parameter. Based on these observations, determine an estimate of & using (a) maximum likelihood (b) method of moments 2....

Q:

3.1. Is it true that (a) N(I) 1? (b) N() snif and only if S, 21? (c) N() > n if and only if S, Note: this information below for answering the question above Renewal Theory 3.1 INTRODUCTION AND...

Q:

Answer the following quesition(partially is also fine) Let U1, U2, ... be a sequence of independent and uniformly distributed random variables on the interval [0, 0]. We interpret 0 > 0 as an unknown...

Q:

1. Let X and Y be independent continuous random variables that are uniformly distributed on (0, 1). Let H = (X + 2) Y. Find the probability P (In H z) where z is a given number that satisfies e

Q:

The number of accidents corresponding to a risk portfolio is a Poisson r.v. with parameter = 1000. The damage sizes for separate accidents are independent r.v.s uniformly distributed on [0,10] (say,...

Q:

The life insurance policy is 2x their yearly salary. She makes $65 000 per year. The cost of this benefit is $1.51 per $1000 of coverage, per month. She is paid bi-weekly. What is the taxable benefit...

Q:

During the school year, the Homebush School band arranges concert dates in many communities. Because only part of the school??s travel expenses are covered by the concert admission fees, the band...

Q:

Under what conditions should you use the pooled-variance t test to examine possible differences in the means of two independent populations?

Q:

Give an example of an unethical business practice that you have personally encountered. LO.1

Q:

What are business processes? How are they related to information systems?

Q:

Identify the management, organization, and technology factors responsible for impeding adoption of internal corporate social networks.

Q:

Compare the experiences implementing internal social networks of the two organizations. Why were they successful? What role did management play in this process?

Q:

Discuss the calculation and recording of the following. Be specific. a) Property taxes b) Compensated absences

Q:

Question 11 The balance sheet is the financial statement most often referred to when analyzing credit risk. a. True. b. False. 4 points Question 12 To avoid potential conflicts of interest, bond...

Q:

EQ2 Q3 Carter takes a short position in a gold forward contract at $1,291 per ounce. On the delivery date, the spot price of gold is 1,286. What is Carter's payoff per ounce?