Let \(X\) be a real-valued random variable on \((\Omega, \mathscr{A}, \mathbb{P})\) and \(\mathscr{F} \subset \mathscr{A}\) be \(\sigma\)-algebra. Show that

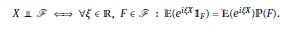
Show that \(\mathbb{E}\left(e^{i \xi X} e^{i \eta \mathbb{1}_{F}}ight)=\mathbb{E}\left(e^{i \xi X}ight) \mathbb{E}\left(e^{i \eta \mathbb{1}_{F}}ight)\) for all \(\xi, \eta \in \mathbb{R}\) and use the characterization of independence by characteristic functions.

XVER, FE(ex 1F) = E(ei)P(F).