The following exercise contains an alternative proof of It's formula (18.1) for a one-dimensional Brownian motion (left(B_{t}
Question:
The following exercise contains an alternative proof of Itô's formula (18.1) for a one-dimensional Brownian motion \(\left(B_{t}\right)_{t \geqslant 0}\).
a) Let \(f \in \mathcal{C}^{1}(\mathbb{R})\). Show that for \(\Pi=\left\{t_{0}=0
Conclude from this that the differential expression \(B_{t} d f\left(B_{t}\right)\) is well-defined.
b) Show that \(d\left(B_{t} f\left(B_{t}\right)\right)=B_{t} d f\left(B_{t}\right)+f\left(B_{t}\right) d B_{t}+f^{\prime}\left(B_{t}\right) d t\).
c) Use (b) to find a formula for \(d B_{t}^{n}, n \geqslant 2\), and show that for every polynomial \(p(x)\) Itô's formula holds:
\[d p\left(B_{t}\right)=p^{\prime}\left(B_{t}\right) d B_{t}+\frac{1}{2} p^{\prime \prime}\left(B_{t}\right) d t .\]
d) Show the following stability result for Itô integrals: \[L^{2}(\mathbb{P})-\lim _{n \rightarrow \infty} \int_{0}^{T} g_{n}(s) d B_{s}=\int_{0}^{T} g(s) d B_{s}\]
for any sequence \(\left(g_{n}\right)_{n \geqslant 1}\) which converges in \(\mathcal{L}_{T}^{2}\).
e) Use a suitable version of Weierstraß' approximation theorem and the stopping technique from the proof of Theorem 18.1, Step \(4^{\circ}\), to deduce from c) Itô's formula for \(f \in \mathcal{C}^{2}\).
Data From 18.1 Theorem
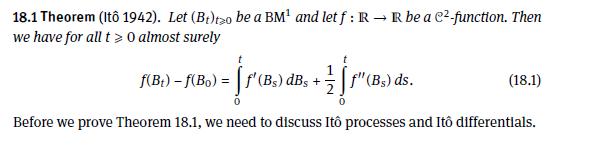
Step by Step Answer:

Brownian Motion A Guide To Random Processes And Stochastic Calculus De Gruyter Textbook
ISBN: 9783110741254
3rd Edition
Authors: René L. Schilling, Björn Böttcher





