A spatial Poisson process is a model for the distribution of points in two dimensional space. For a set A R 2 , let N

A spatial Poisson process is a model for the distribution of points in two dimensional space. For a set A Š† R², let N_Adenote the number of points in A. The two defining properties of a spatial Poisson process with parameter λ are

1. If A and B are disjoint sets, then N_A and N_B are independent random variables.
2. For all A Š† R², N_A has a Poisson distribution with parameter λ|A| for some λ > 0, where |A| denotes the area of A. That is,

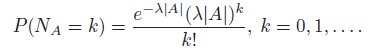
Consider a spatial Poisson process with parameter λ. Let x be a fixed point in the plane.
(a) Find the probability that there are no points of the spatial process that are within two units distance from x. (Draw the picture.)
(b) Let X be the distance between x and the nearest point of the spatial process. Find the density of X. (Find P(X > x).)

e-Al (4|)* k = 0,1, .... P(NA= k) = k!