Question: Let X be a random variable, not necessarily positive. (a) Using Markovs inequality, show that for x > 0 and t > 0, assuming that

Let X be a random variable, not necessarily positive.
(a) Using Markov€™s inequality, show that for x > 0 and t > 0, E[e=] = e -t=m(t), P(X > x) < etr (9.5)

assuming that E[e^tx] exists, where m is the mgf of X.

(b) For the case when X has a standard normal distribution, give the upper bound in Equation 9.5. Note that the bound holds for all t > 0.
(c) Find the value of t that minimizes your upper bound. If Z ˆ¼ Norm(0,1), show that for z > 0,

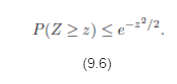
P(Z > =) <e==³/2. =² /2 (9.6)

The upper bounds in Equations 9.5 and 9.6 are called Chernoff bounds.

E[e=] = e -t=m(t), P(X > x) < etr (9.5) P(Z > =)

Step by Step Solution

★★★★★

3.48 Rating (151 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Let X Binomn n Then The limit is t... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Probability With Applications Questions!

Let X be a random variable taking on values a1, a2, . . . , pr with probabilities p1, p2, . . . , pr and with E(X) = μ. Define the spread of X as follows: This, like the standard deviation, is a...

Let X be a random variable that takes on nonnegative values and has distribution function F(x). Show that Hint: Integrate by parts. Illustrate this result by calculating E(X) by this method if X has...

Let X be a random variable taking on values a1, a2, . . . , pr with probabilities p1, p2, . . . , pr and with E(X) = μ. Define the spread of X as follows: This, like the standard deviation, is a...

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

Consider the Markov Chain, Xn, on the states i = 0, 1, 2, . . . with transition matrix given by pi,i1 = p i = 1, 2, . . . pi,i+1 = 1 p i = 0, 1, . . . p0,0 = p where 0

5 Just One Tail, Please 5 Just One Tail, Please Let X be some random variable with nite mean and variance which is not necessarily non- negative. The extended version of Markov's Inequality states...

lup ] (d) Show how a generating (or "mother") wavelet (x) can spawn a family of "daughter" wavelets jk(x) by simple shifting and scaling operations, and explain the advantages of representing...

Set Student Name: 1. Describe the relationship between two variables that have a correlation coefficient value: a. Near -1 b. Near 0 c. Near 1 2. Data was collected where a weightlifter was asked to...

Instuctor's Annotated Edition TENTH EDITION Understandable Statistics Concepts and Methods Charles Henry Brase Regis University Corrinne Pellillo Brase Arapahoe Community College Australia Brazil...

1 Just One Tail, Please Let X be some random variable with nite mean and variance which is not necessarily non- negative. The extended version of Markov's Inequality states that for a non-negative,...

Roy continued his business in October 2021 and his bank account was given as follows: Details Balance b/d Sales Ahmad 24 Rathi 28 Rental 29 Daya Ltd Date Oct 1 12 22 Date Oct-01 Balance 6 Cheque RM...

How is International Business and Trade (Global Marketing) related to your future career as an accountant? How would you expect yourself to come into contact with global business and trade?

The real quantity of money is I. equal to M/P. II. the money supply adjusted for inflation. III. higher in the long run when the Fed buys government securities. a. I only b. II only c. III only d. I...

What would be Simones first steps to address the issue she identified? Would she need some help? From whom?

Suppose we wanted a 99% CI. Would this interval be longer, shorter, or the same size as the 95% CI in Problem 8.152? (Do not actually compute the interval.) Diabetes The insulin pump is a device that...

Provide a 95% CI for the mean change in heart rate after using the treadmill for 5 minutes. The subject also recorded his heart rate at baseline and 5 minutes after starting treadmill exercise (at a...

Implement a test to compare the baseline heart rate initially (2000) and after 10 years of exercise (2010), and report a two-sided p-value? The subject also recorded his heart rate at baseline and 5...

k . $ 1 , 0 0 0 , 1 0 % annual rate loan with three equal installments. During Year 2 , what is the annual interest expense for the borrower, and what is the annual interest income for the lender?

For the most recent year available, the mean annual cost to attend a private university in the United States was $42,224. Assume the distribution of annual costs follows the normal probability...

Based on asurvey, assume that 41% of consumers are comfortable having drones deliver their purchases. Suppose that we want to find the probability that when five consumers are randomlyselected,...