For the system in exercise 3, write down the equation of motion for \(x_{1}^{2}+x_{2}^{2} \equiv r^{2}\) and then the corresponding Ehrenfest theorem equation and its transformed version under the continuous symmetries, in both the active and the passive sense.

Data From Exercise 3:-

Consider two harmonic oscillators of the same mass and frequency, with Hamiltonian

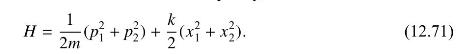
Find the continuous symmetries of the system and write down the resulting conserved charges as a function of the phase space variables. Then quantize the system, and show that the charges do indeed commute with the quantum Hamiltonian.

HP++ H = 2m k + P) + (x + x). (12.71)