Question: Let X = [X 1 X 2 ] T denote a bivariate normal. (Gaussian) random vector. Assume and Define Y l = X 1 +
Let X = [X 1 X 2 ] T denote a bivariate normal. (Gaussian) random vector. Assume ![EX = 0 EXXT = [1].](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2022/08/63078de0d6325_45663078de0bf20a.jpg){kind=small}
and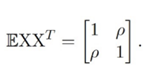 
Define Y l = X 1 + X 2 and Y2 = -X 1 + X 2
1. Find the joint distribution of Y 1 and Y 2 ; find the marginal distributions of Y l and Y2.
2. Find the conditional density of X l , given Y l ; find the conditional density of X l , given Y2.
3. Find the conditional mean and variance of X 1 , given Y l ; find the conditional mean and variance of X l , given Y 2 .
EX = 0 EXXT = [1].
Step by Step Solution
3.56 Rating (170 Votes )
There are 3 Steps involved in it
To solve this problem we consider X beginbmatrix X1 X2 endbmatrix as a bivariate normal vector with mean mathbfEX beginbmatrix 0 0 endbmatrix and cova... View full answer
Get step-by-step solutions from verified subject matter experts
Document Format (2 attachments)
609502c79259e_25457.pdf
180 KBs PDF File
609502c79259e_25457.docx
120 KBs Word File
Study Help