The current i _C in a capacitor is given by:

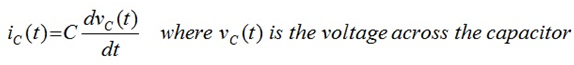
The voltage v _L across an inductor is given by:

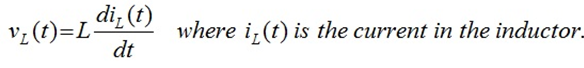
The voltage across the capacitor cannot changed instantaneously, and the capacitor is uncharged. In the circuit of figure 1, the switch is initially at position 1, and the capacitor is uncharged.

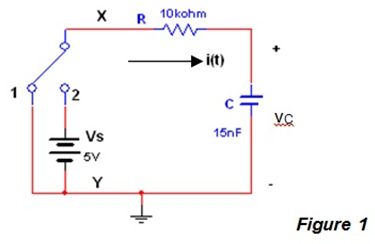
At t = 0, the switch is flipped to position 2 which connects V _s to the RC circuit. The capacitor charges up, and its voltage increases exponentially towards V _s , with a time constant i _c = RC).

After one millisecond, the switch is put back into position 1. The capacitor now discharges, and its voltage decreases exponentially towards 0V.

The switch is toggled at this rate between the two pole positions.

For the charging interval, at t=i(assuming at t=0, v _C (0) = 0V), v _C (i) = 0.632 *V _s = 3.16 V (for V _s = 5 V).

For the discharging interval, at t=i(assuming at t=0, v _C (0) = V _s ), v _C (i) = 0.368 *V _s = 1.84 V (for V _s = 5 V).

For Figure 1 find its time constant and complete the table below

ic (t)=C dvc (t) dt where ve(t) is the voltage across the capacitor V (t)=L diz(t) v dt where i(t) is the current in the inductor. 92 X R 10kohm Vs 5V Y i(t) 15nF VC Figure 1 Time 0- 0+ Current i(t) Voltage across the capacitor vc i(0-) = vc(0-) = i(0+) = 0.3ms (0.3ms) = vc(0+) = Table 1 vc(0.3ms) = Voltage across the resistor VR VR(0-) = VR(0+) = VR(0.3ms) = Change in voltage across the capacitor w.r.t. time dvc -(0)= dt dvc dt dvc dt -(0*)= (0.3ms)=