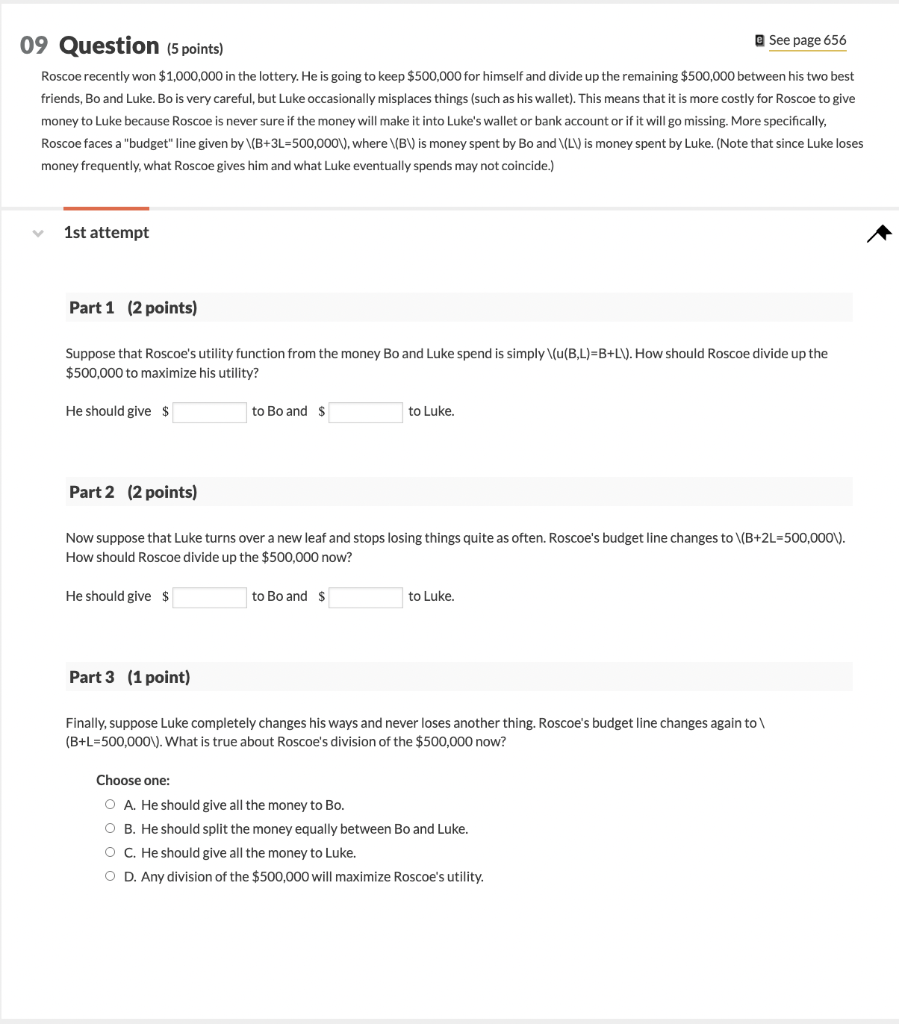
09 Question (5 points) See page 656 Roscoe recently won $1,000,000 in the lottery. He is going to keep $500,000 for himself and divide up the remaining $500,000 between his two best friends, Bo and Luke. Bo is very careful, but Luke occasionally misplaces things (such as his wallet). This means that it is more costly for Roscoe to give money to Luke because Roscoe is never sure if the money will make it into Luke's wallet or bank account or if it will go missing. More specifically, Roscoe faces a "budget" line given by \(B+3L=500,000V), where (BV is money spent by Bo and ((LV) is money spent by Luke. (Note that since Luke loses money frequently, what Roscoe gives him and what Luke eventually spends may not coincide.) V 1st attempt Part 1 (2 points) Suppose that Roscoe's utility function from the money Bo and Luke spend is simply \(u(B,L)=B+L\). How should Roscoe divide up the $500,000 to maximize his utility? He should give $ to Bo and $ to Luke. Part 2 (2 points) Now suppose that Luke turns over a new leaf and stops losing things quite as often. Roscoe's budget line changes to \(B+2L=500,000V). How should Roscoe divide up the $500,000 now? He should give $ to Bo and $ to Luke. Part 3 (1 point) Finally, suppose Luke completely changes his ways and never loses another thing. Roscoe's budget line changes again to (B+L=500,000V). What is true about Roscoe's division of the $500,000 now? Choose one: O A. He should give all the money to Bo. O B. He should split the money equally between Bo and Luke. O C. He should give all the money to Luke. O D. Any division of the $500,000 will maximize Roscoe's utility. 09 Question (5 points) See page 656 Roscoe recently won $1,000,000 in the lottery. He is going to keep $500,000 for himself and divide up the remaining $500,000 between his two best friends, Bo and Luke. Bo is very careful, but Luke occasionally misplaces things (such as his wallet). This means that it is more costly for Roscoe to give money to Luke because Roscoe is never sure if the money will make it into Luke's wallet or bank account or if it will go missing. More specifically, Roscoe faces a "budget" line given by \(B+3L=500,000V), where (BV is money spent by Bo and ((LV) is money spent by Luke. (Note that since Luke loses money frequently, what Roscoe gives him and what Luke eventually spends may not coincide.) V 1st attempt Part 1 (2 points) Suppose that Roscoe's utility function from the money Bo and Luke spend is simply \(u(B,L)=B+L\). How should Roscoe divide up the $500,000 to maximize his utility? He should give $ to Bo and $ to Luke. Part 2 (2 points) Now suppose that Luke turns over a new leaf and stops losing things quite as often. Roscoe's budget line changes to \(B+2L=500,000V). How should Roscoe divide up the $500,000 now? He should give $ to Bo and $ to Luke. Part 3 (1 point) Finally, suppose Luke completely changes his ways and never loses another thing. Roscoe's budget line changes again to (B+L=500,000V). What is true about Roscoe's division of the $500,000 now? Choose one: O A. He should give all the money to Bo. O B. He should split the money equally between Bo and Luke. O C. He should give all the money to Luke. O D. Any division of the $500,000 will maximize Roscoe's utility