$(10$ points$)$ The InDEPEnDEnT$-$SET problem is defined as follows:

Given a graph $G$ and a positive integer $k,$ accept $($:$G,k$:$)$ if $G$

contains a subset of vertices $V^{\text{'}}$ such that $|V^{\text{'}}|=k$ and $V^{\text{'}}$

is an independent set $-$ i$.$e$.,$ for any two vertices $u,vin{V}^{\text{'}},$

$(u,v)!$inE.

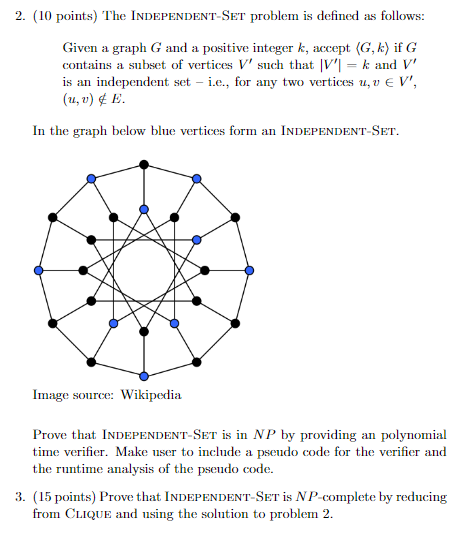
In the graph below blue vertices form an INDEPENDENT$-$SET.

Prove that INDEPENDENT$-$SET is in $NP$ by providing an polynomial

time verifier. Make user to include a pseudo code for the verifier and

the runtime analysis of the pseudo code.

$(15$ points$)$ Prove that INDEPENDENT$-$SET is $NP-$complete by reducing

from Clique and using the solution to problem $2.$