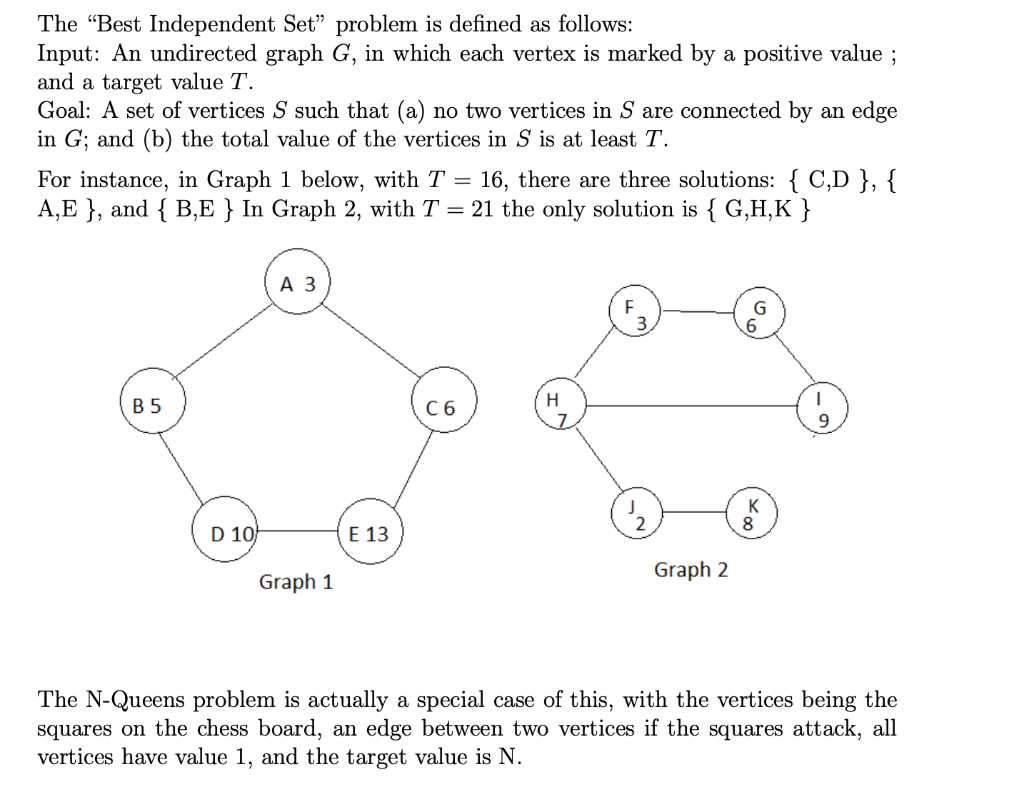
The "Best Independent Set" problem is defined as follows: Input: An undirected graph G, in which each vertex is marked by a positive value ; and a target value T. Goal: A set of vertices S such that (a) no two vertices in S are connected by an edge in G; and (b) the total value of the vertices in S is at least T. For instance, in Graph 1 below, with T=16, there are three solutions: { C,D },{ A,E}, and {B,E} In Graph 2, with T=21 the only solution is {G,H,K} The N-Queens problem is actually a special case of this, with the vertices being the squares on the chess board, an edge between two vertices if the squares attack, all vertices have value 1 , and the target value is N. Consider the Best Independent Set on a graph in general with n vertices (not on the specific examples above). What is the maximal depth D of the state space? What is the branching factor B ? Give a bound on the number of states in the state space (you should be able to get a bound much smaller than BD.)