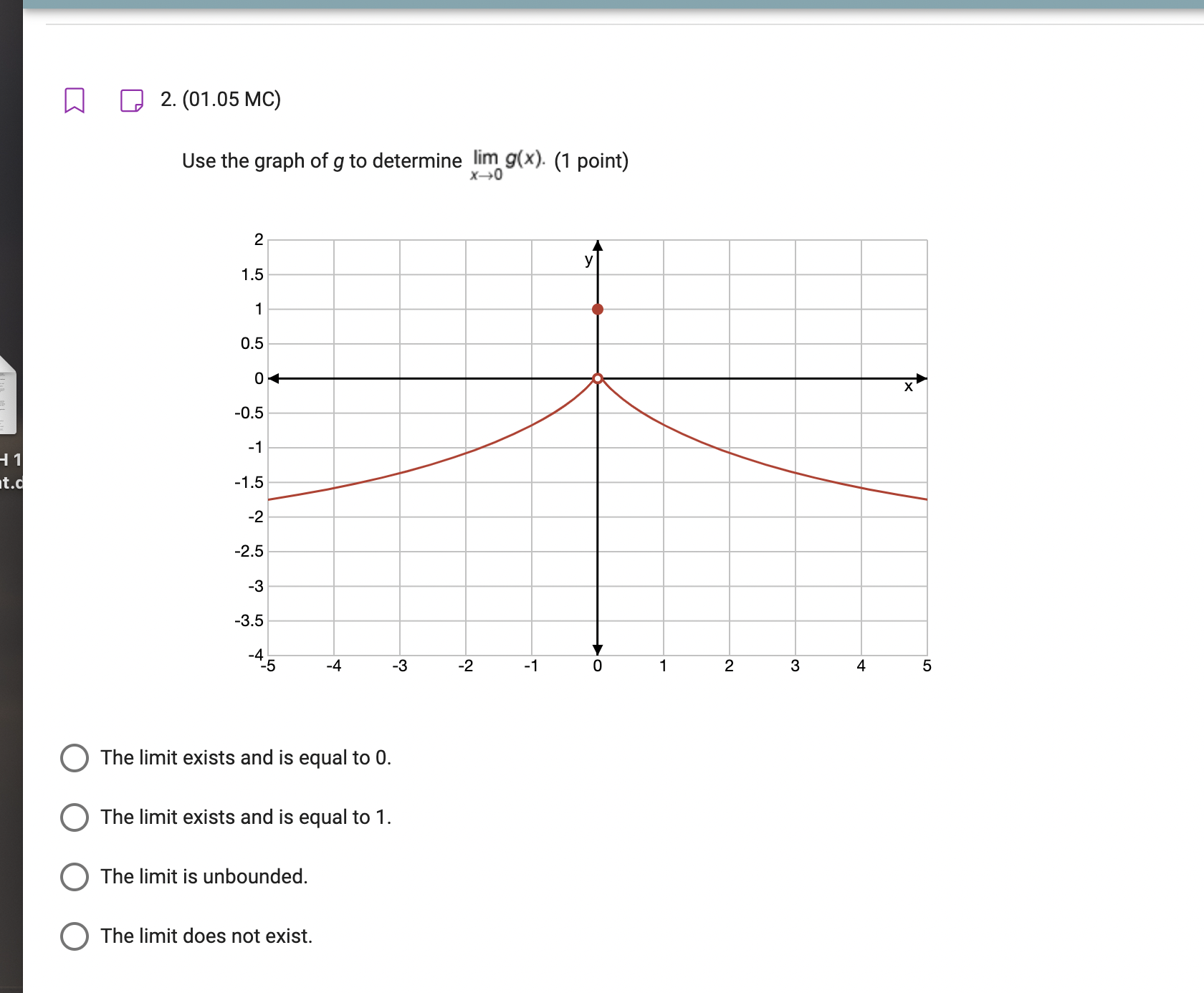
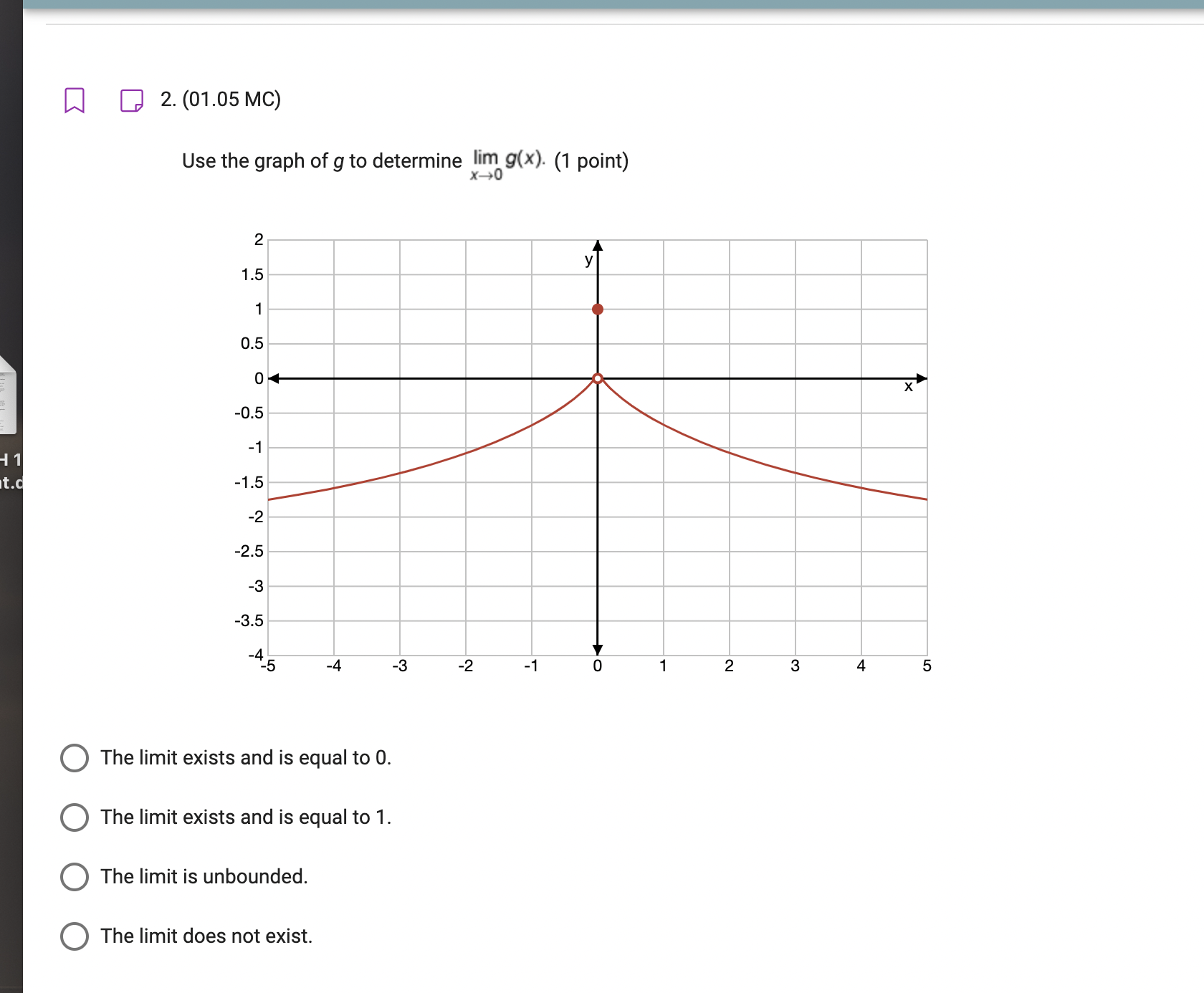
1. (01.05 MC) sin x If h(x) = then lim h(x) is equivalent to which of the following? (1 point) sin 2x O N O o O 1 O Does not exist[I] [3 2. (01.05 MC) Use the graph of g to determine 909\")- (1 point) 0 The limit exists and is equal to 0. O The limit exists and is equal to 1. O The limit is unbounded. O The limit does not exist. m D 3.(01.05MC) 0052 x sin 2x ' Which of the following accurately describes the limit as x approaches 0 ofthe function? (1 point) Consider the function 000 = 0 As x approaches 0, the limit of p(x) approaches a large negative yvalue. Q As x approaches 0, the limit of p(x) does not exist. 0 As x approaches 0, the limit ofp(x) approaches 0. Q As x approaches 0, the limit of p(x) approaches a large positive y-value. a D 4. (01.05 MC) 2 Determine which statement BEST describes Iim WA ( XDl X _1 1 point) 0 The limit is does not exist because there is a hole when x = 1. O The limit does not exist because it is unbounded. O The limit exists and is equal to 0. O The limit exists and is equal to 1. Q 5. (01.05 MC) H 1 nt.q x2 - x-2 if x 2 Find lim f(x). (1 point) x-2 Does not exist O -3 O Al- O 3