1.

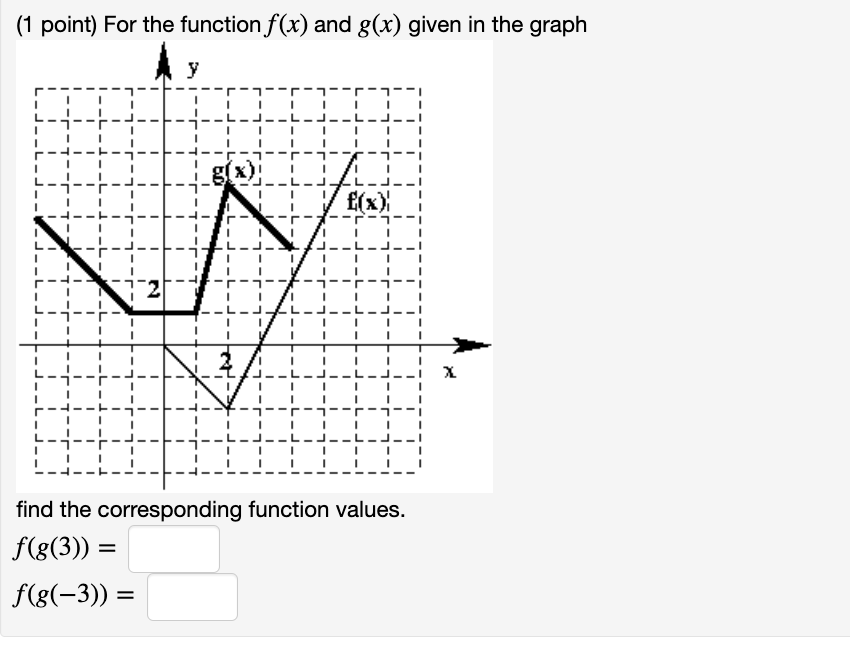
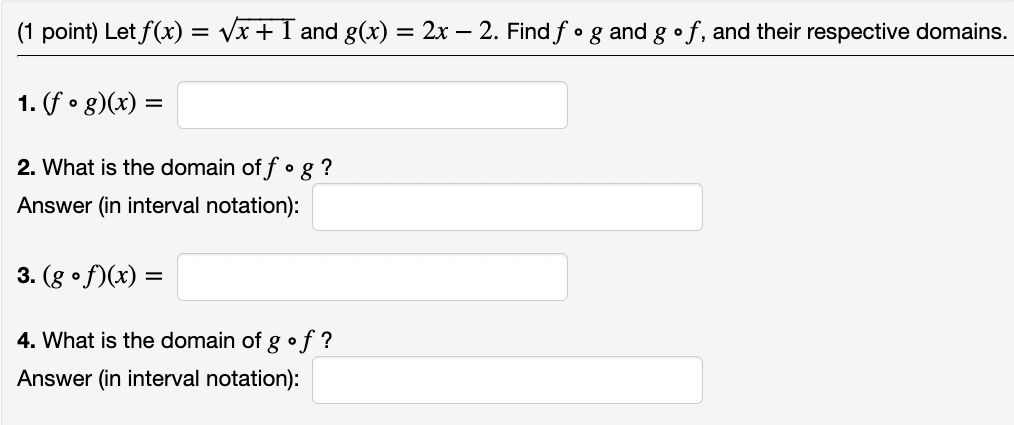
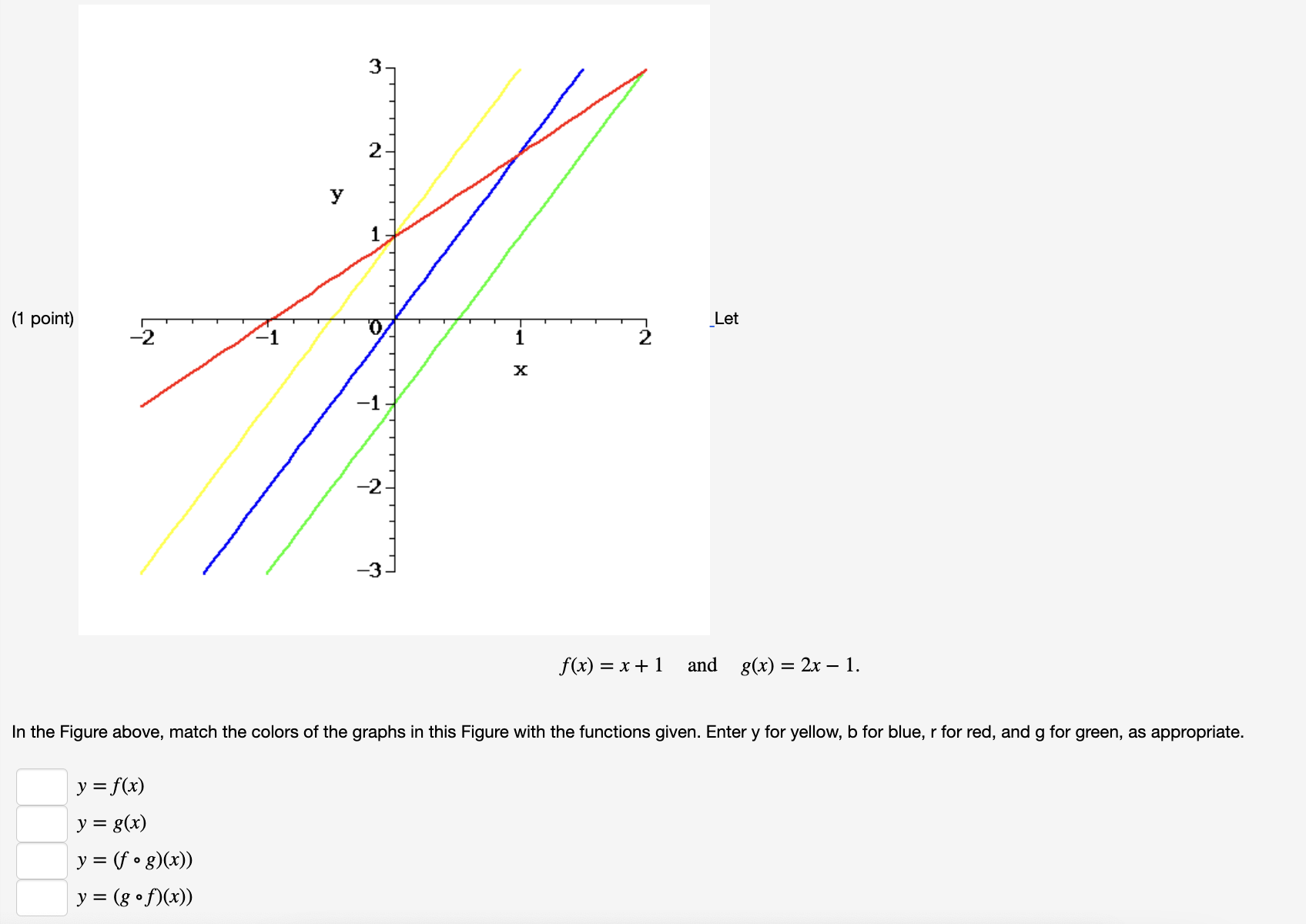
(1 point) For the function f(x) and g(x) given in the graph Y E(x) 2 X find the corresponding function values. f(8(3)) = f(8(-3)) =\f\f(1 point) Let f(x) = Vx + 1 and g(x) = 2x 2. Find f o g and g o f, and their respective domains. 1- (fg)(x) = 2. What is the domain of f o g ? Answer (in interval notation): 3- (8 (x) = 4. What is the domain of g of ? Answer (in interval notation): _Let f(x)=x+1 and g(x)=2x1. In the Figure above, match the colors of the graphs in this Figure with the functions given. Enter y for yellow, b for blue, r for red, and g for green, as appropriate. y = f(x) y = 306) y = (f 906)) y = (3 9906)) (2 points) Given that f(x) = i and g(x) = 7x + 2, calculate (a) f o g(x)= , its domain is all real numbers except (b) g f(x)= , its domain is all real numbers except (c) f o f(x)= , its domain is all real numbers except (d) g 8(x)= , its domain is ( Note: If needed enter co as infinity and 00 as -innity . (2 points) Let f be the linear function (in blue) and let g be the parabolic function (in red) below. If you are having a hard time seeing the picture clearly, click on the picture. It will expand to a larger picture on its own page so that you can inspect it more closely. Note: If the answer does not exist, enter 'DNE': 1. (f o g)( 2 ) = 2. (g o f) ( 2 ) = 3. (f o f) ( 2 ) = 4. (g o g)( 2 ) = 5. (f + 9)( 4 ) = 6. (f / g)( 2 ) =(1 point) Suppose you are exchanging currency in the London airport. The currency exchange service there only makes transactions in which one of the two currencies is British pounds, but you want to exchange dollars for Euros. Thus you rst need to exchange dollars for British pounds, then exchange British pounds for Euros. At the time you want to make the exchange, the function f for exchanging dollars for British pounds is give by the formula f(d) = 0.65d 1 and the function g for exchanging British pounds for Euros is given by the formula g(p) = 1.25p 2. (The subtraction of 1 or 2 in the number of British pounds or Euros that you receive is the fee charged by the currency exchange service for each transaction.) a) Find a formula for the function that exchanges dollars in return for Euros. Exchange function: b) How many Euros would you receive for exchanging 400 dollars after going through this two-step exchange process? Answer: Euros c) How many dollars would you need to exchange in order to end up with 60 Euros after this two-step exchange process? Answer: dollars (1 point) The area of a circular wave expands across a still pond such that its radius increases by 14 cm each second. Write a formula for the area A of the circle as a function of time t since the wave begin5:A =