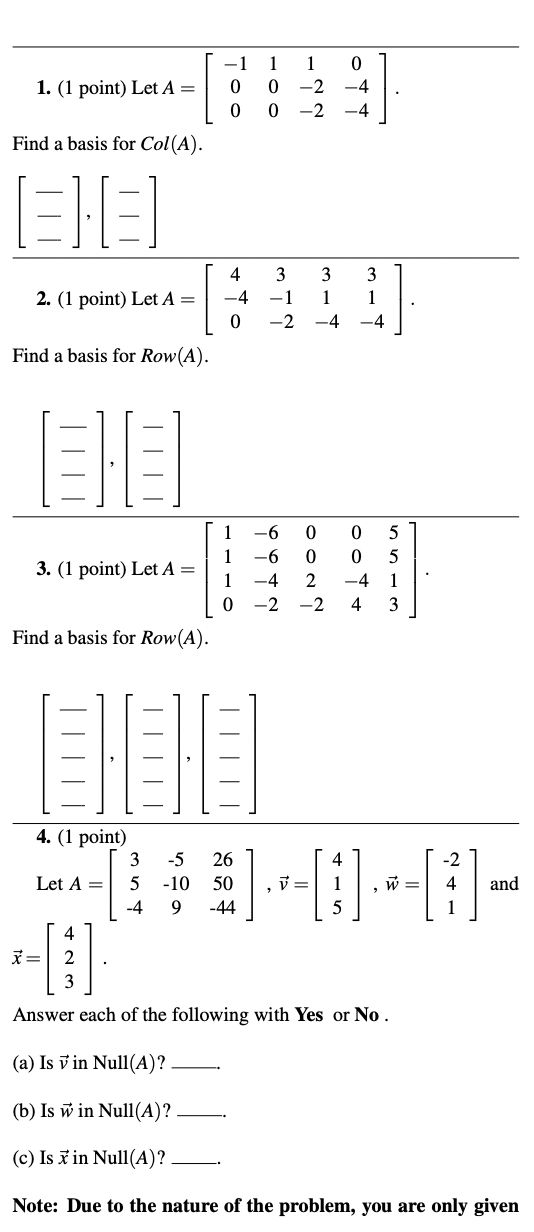
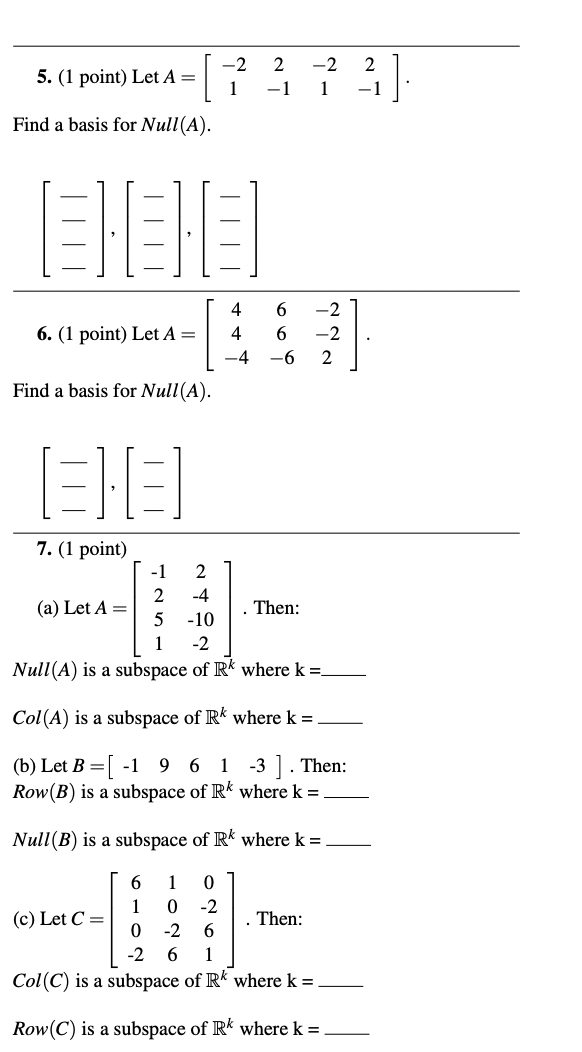
1. (1 point) Let A = Find a basis for Col(A). 2. (1 point) Let A = -4 -2 -4 Find a basis for Row(A). 3. (1 point) Let A = NNOO ALOO OH - Find a basis for Row(A). 4. (1 point) -5 26 NO Let A = A UI w -10 50 V= W= 4 and 9 -44 X = W N Answer each of the following with Yes or No . (a) Is v in Null(A)? (b) Is w in Null(A)? (c) Is x in Null(A)? Note: Due to the nature of the problem, you are only given-2 5. (1 point) Let A = 2 - N -1 Find a basis for Null(A). 4 6 6. (1 point) Let A = 4 6 -6 Find a basis for Null(A). 7. (1 point) N -4 (a) Let A = UN . Then: -10 -2 Null(A) is a subspace of RK where k =_ Col(A) is a subspace of R* where k = (b) Let B = [ -1 9 6 1 -3 ]. Then: Row(B) is a subspace of RK where k = Null(B) is a subspace of Rk where k = 6 O 0 (c) Let C = . Then: -2 6 -2 6 Col(C) is a subspace of R* where k = Row(C) is a subspace of R* where k =8. (1 point) (c) Is * in Null(A)? Let 7 : R2 -> IR be a matrix transformation for which: Note: Due to the nature of the problem, you are only given 11. (1 point) Let 7 : R' - R- be a matrix transformation with standard matrix Using the properties of a matrix transformations, determine the following: Let M : R2 -> IR2 be a matrix transformation with standard ma- trix [ = ] 3= 3 3] Determine the standard matrix C of the composition Mo T. (b)7(-7) =[=] (C)T (3u - 7v) [=] Reminder: In general, (M . T) (x) = M(T (x)). 12. (1 point) Determine the standard matrix A of the matrix transforma- 9. (1 point) Let 7 : R - R' be a matrix transformation for tion 7 : R- - R- that rotates any vector through an angle of 60 which: in the counterclockwise direction. 13. (1 point) Determine the standard matrix C that first reflects a point about the x1-axis (or x-axis) and then reflects the point about the Determine the standard matrix A of T. line x2 = -x1 (or y = -x). [Note: The reflection through y = -x transforms [x,y] to [-y, -x]' .] 10. (1 point) Let 7 : R R" be the linear (matrix) transfor- mation defined by: 14. (1 point) T(x1,x2) = (-X1 - 8x2, 7x1 - 9x2, -6x2, 3x1 + 5x2). Determine the standard matrix B that first rotates a point clockwise through - radians and then reflects the point about Determine the standard matrix A of the linear transformation. the line x2 = x1 (or y = x). [Note: The reflection through y = x transforms [x, y]] to [y,x]7 .] A= B- [= =]