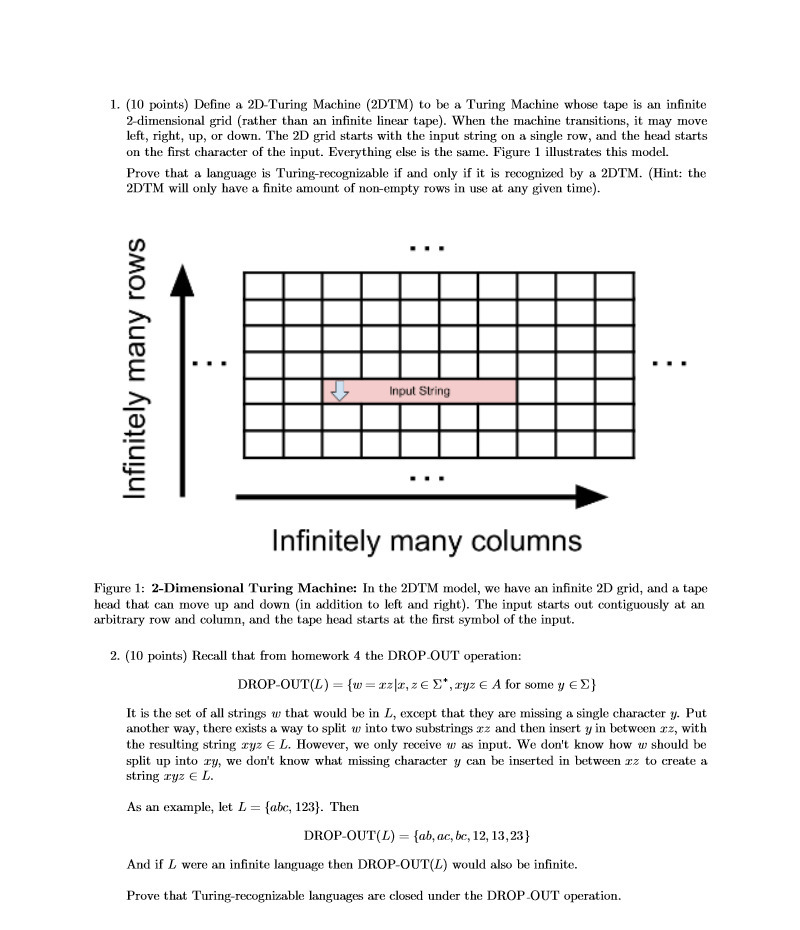
Question: 1. (10 points) Define a 2D-Turing Machine (2DTM) to be a Turing Machine whose tape is an infinite 2-dimensional grid (rather than an infinite linear
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


