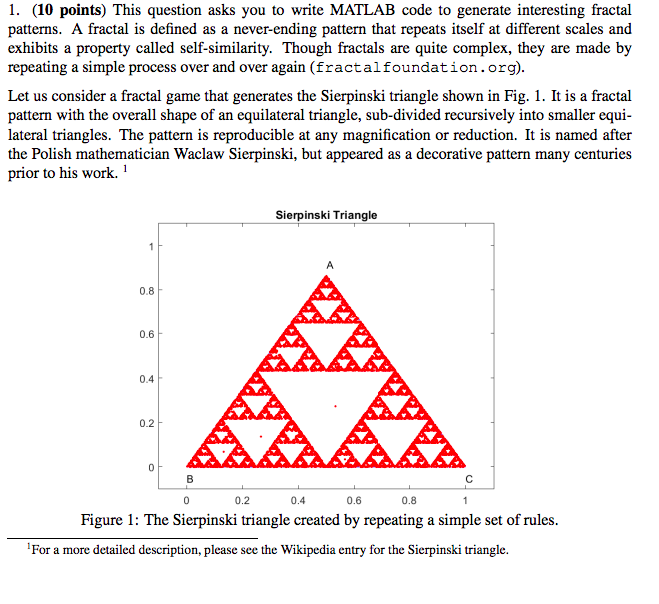
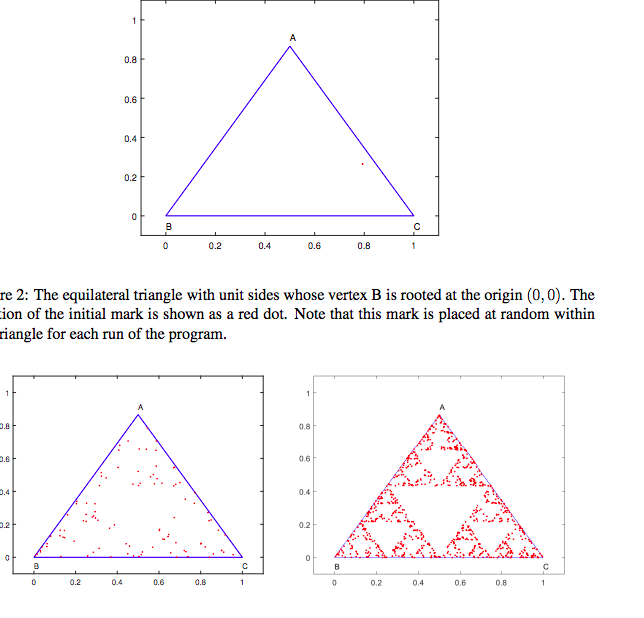
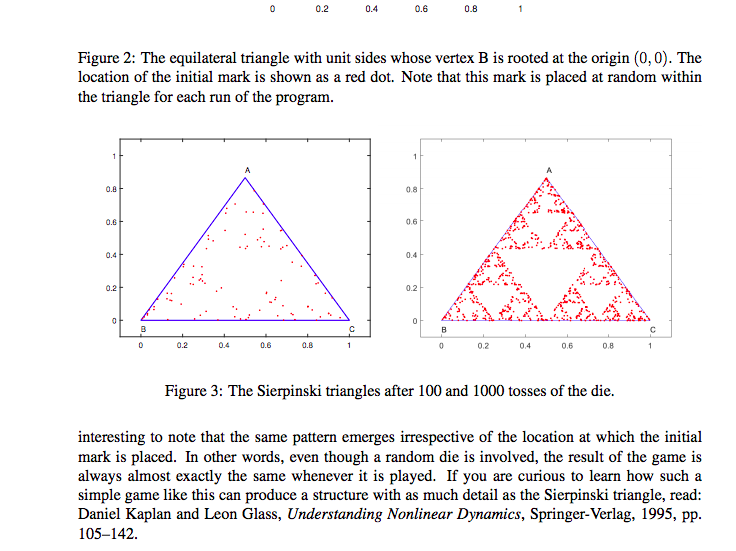
1. (10 points) This question asks you to write MATLAB code to generate interesting fractal patterns. A fractal is defined as a never-ending pattern that repeats itself at different scales and exhibits a property called self-similarity. Though fractals are quite complex, they are made by repeating a simple process over and over again (fractalfoundation.org). Let us consider a fractal game that generates the Sierpinski triangle shown in Fig. 1. It is a fractal pattern with the overall shape of an equilateral triangle, sub-divided recursively into smaller equi lateral triangles. The pattern is reproducible at any magnification or reduction. It is named after the Polish mathematician Waclaw Sierpinski, but appeared as a decorative pattern many centuries prior to his work.1 Sierpinski Triangle 0.8 0.6 0.4 0.2 0.2 0.4 0.6 0.8 Figure 1: The Sierpinski triangle created by repeating a simple set of rules For a more detailed description, please see the Wikipedia entry for the Sierpinski triangle. 1. (10 points) This question asks you to write MATLAB code to generate interesting fractal patterns. A fractal is defined as a never-ending pattern that repeats itself at different scales and exhibits a property called self-similarity. Though fractals are quite complex, they are made by repeating a simple process over and over again (fractalfoundation.org). Let us consider a fractal game that generates the Sierpinski triangle shown in Fig. 1. It is a fractal pattern with the overall shape of an equilateral triangle, sub-divided recursively into smaller equi lateral triangles. The pattern is reproducible at any magnification or reduction. It is named after the Polish mathematician Waclaw Sierpinski, but appeared as a decorative pattern many centuries prior to his work.1 Sierpinski Triangle 0.8 0.6 0.4 0.2 0.2 0.4 0.6 0.8 Figure 1: The Sierpinski triangle created by repeating a simple set of rules For a more detailed description, please see the Wikipedia entry for the Sierpinski triangle