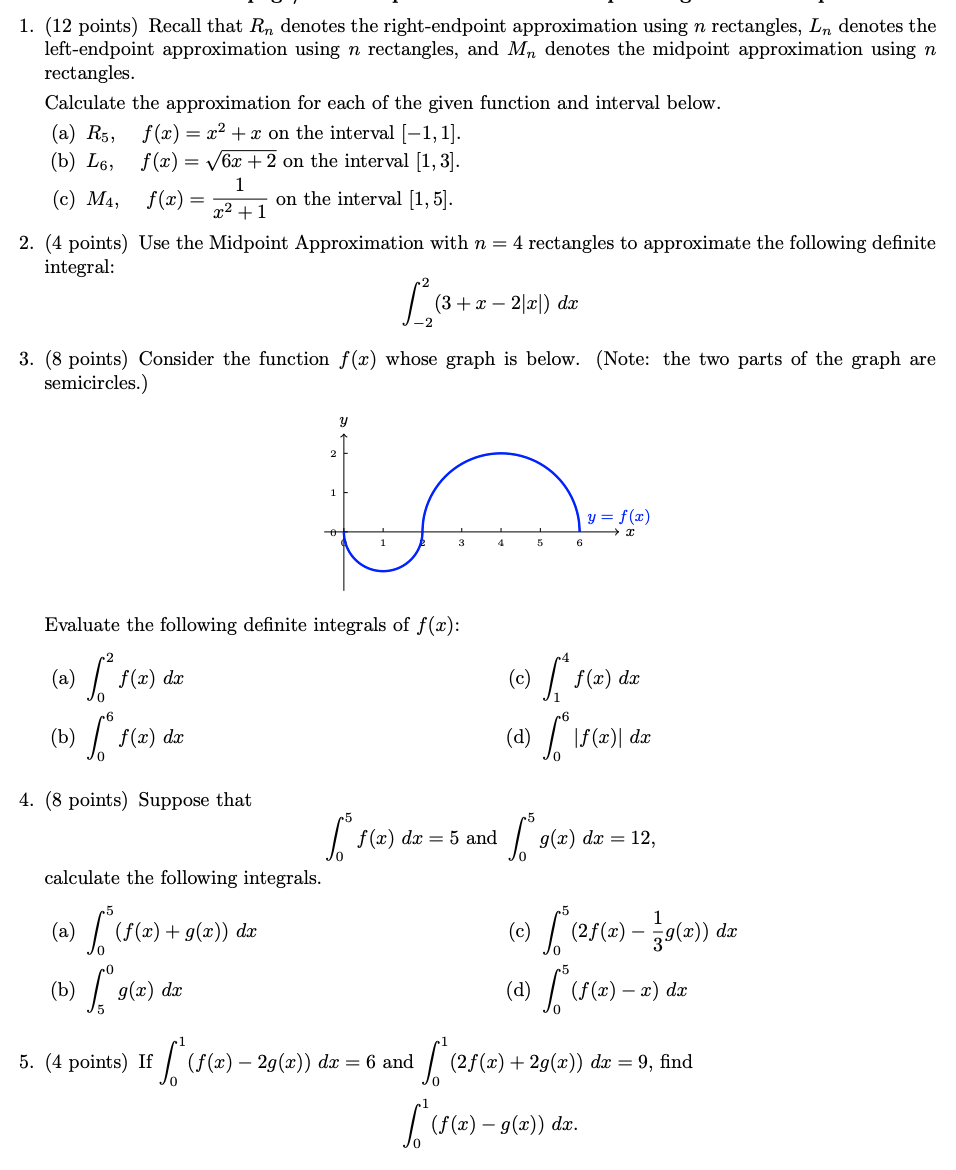
1. (12 points) Recall that An denotes the right-endpoint approximation using n rectangles, In denotes the left-endpoint approximation using n rectangles, and M, denotes the midpoint approximation using n rectangles. Calculate the approximation for each of the given function and interval below. (a) Rs, f(x) = x2 + x on the interval [-1, 1]. (b) L6, f(x) = V6x + 2 on the interval [1, 3]. (c) MA, f(x) = - x2 + 1 on the interval [1, 5]. 2. (4 points) Use the Midpoint Approximation with n = 4 rectangles to approximate the following definite integral: [,(3+2-2121) da 3. (8 points) Consider the function f(x) whose graph is below. (Note: the two parts of the graph are semicircles.) y = f(x) Evaluate the following definite integrals of f(x): ( a ) [ f ( z ) da (c ) [ f ( 2 ) da (a ) [if(ell da 4. (8 points) Suppose that J." f(x) do = 5 and J o(x) de = 12, calculate the following integrals. ( 2 ) 1 ( s ( ) + 9 ( 2 ) ) de ( ) 1 0 (28 ( ) - 30 ( 2 ) da (a) [ (f(x ) - 2) de If [" (s(x ) - 29(2) du = 6 and [" (25(x) + 29(2) da = 9, find [(f(x) -9(2)) de