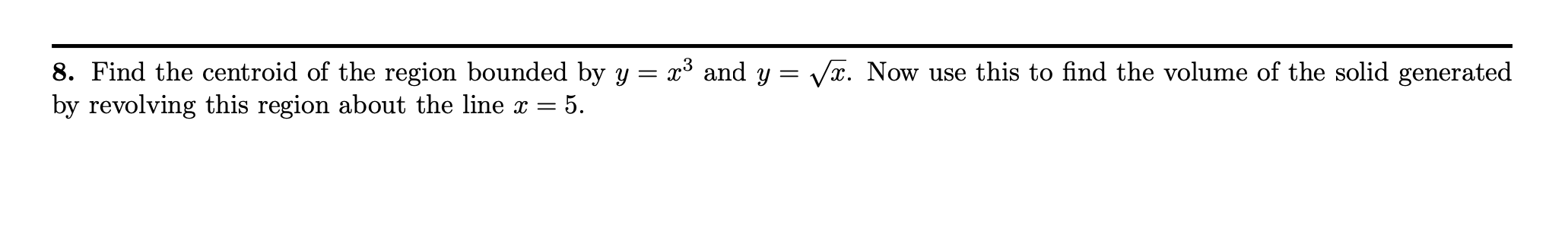
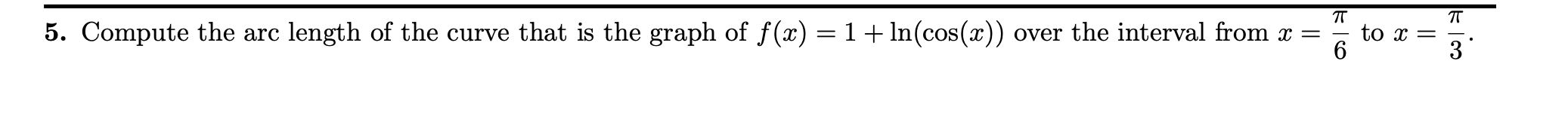
1 15. Part 3: Consider the function f (3:) = i on the interval a: E [1, 00). Using proper limit notation, Show that the area m between the graph of f() and the S's-axis is innite yet the volume generated by revolving this region about the maxis is nite. 1 15. Part b: Consider the function f (9:) = on the interval as E [1, 00). Using proper limit notation, show that the surface 9: area of the solid formed by revolving this curve about the xaxis is innite. (Hint: if a > 0 then x/ 1 + a > 1.) 8. Find the centroid of the region bounded by y = x3 and y = . Now use this to nd the volume of the solid generated by revolving this region about the line a: = 5. 5. Compute the arc length of the curve that is the graph of f(x) = 1 + In(cos(x)) over the interval from x = to C =