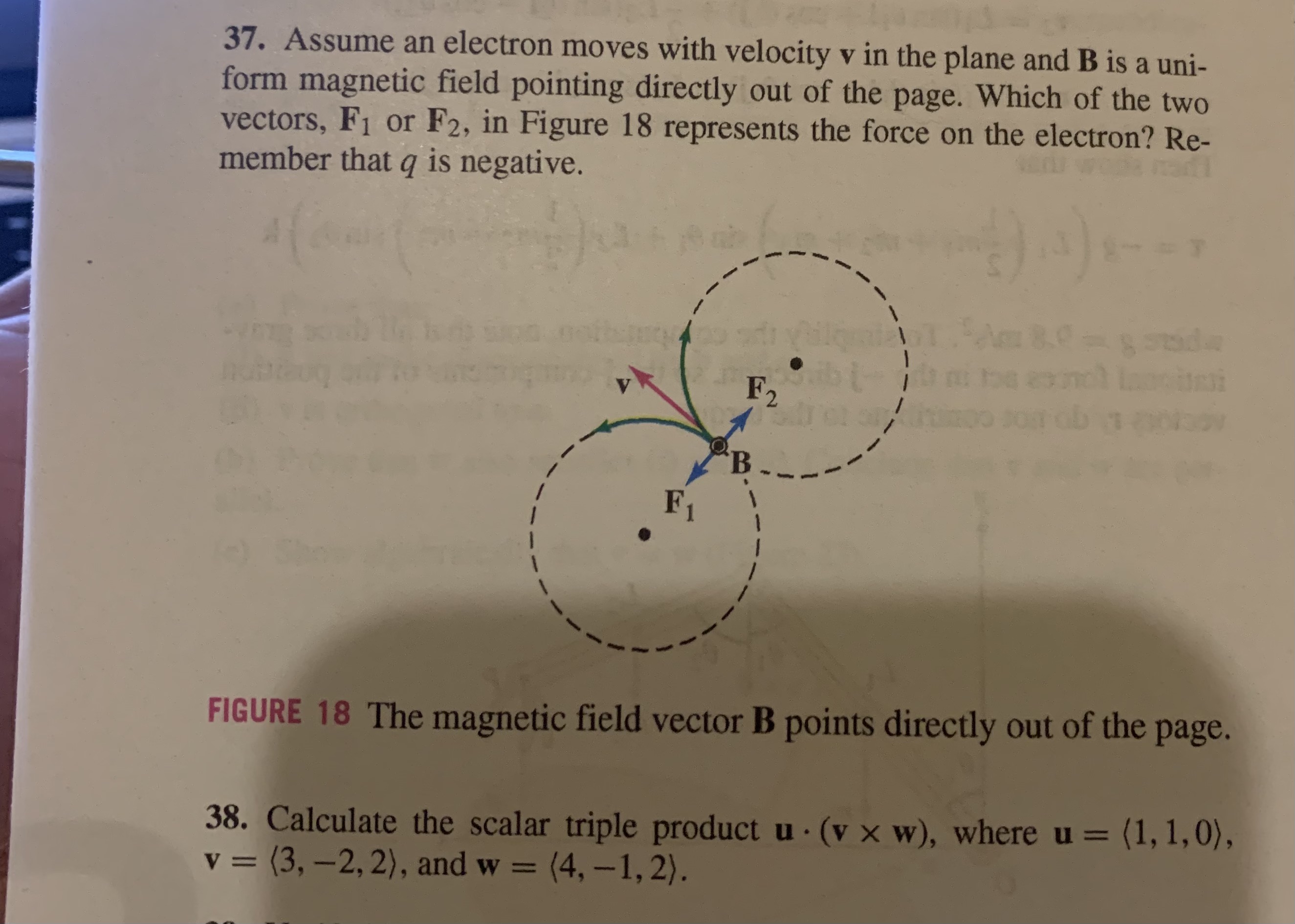
(-1, 2, 1). 33. Let e and e' be unit vectors in R' such that e _ e'. Use the geometric properties of the cross product to compute e x (ex e).37. Assume an electron moves with velocity v in the plane and B is a uni- form magnetic field pointing directly out of the page. Which of the two vectors, F1 or F2, in Figure 18 represents the force on the electron? Re- member that q is negative. F FIGURE 18 The magnetic field vector B points directly out of the page. 38. Calculate the scalar triple product u . (v x w), where u = (1, 1, 0), v = (3, -2, 2), and w = (4, -1, 2).40. Find the volume of the parallelepiped spanned by u, v, and w in Figure 19. 41. Find the area of the parallelogram spanned by v and w in Fig- ure 19.44. Sketch the parallelogram spanned by u = (1, 1, 1) and v = (0,0,4). and compute its area. 45. Calculate the area of the parallelogram spanned by u = (1,0,3) and v = (2, 1, 1). at 46. Find the area of the parallelogram determined by the vectors (a, 0,0) is and (0, b, c). e 47. Sketch the triangle with vertices at the origin O, P = (3,3,0), and Q = (0, 3, 3), and compute its area using cross products. 48. Use the cross product to find the area of the triangle with vertices P = (1, 1,5), Q = (3, 4, 3), and R = (1, 5, 7)