(1)

(2)

(3)

(4)

(5)

(6)

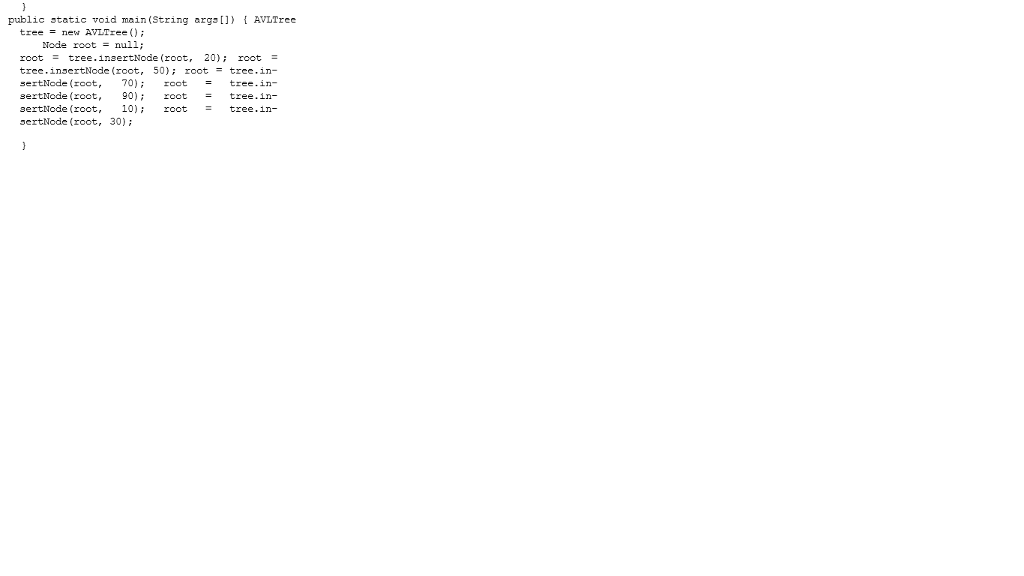
Fill in the missing parts of this java code where you find #code here, such that it will:

1-Implement a recursive Java Method TreeHeight()for finding the height of a binary search tree. The height of a binary search tree is the length of the longest path from the root to a leaf.Hint: Modify your Java Method PrintTree() to determine the height of each nodes left and right subtree.

Example: use the same nodes in the main method Output: 4

2-compute the balance factor for each subtree getBalance() and prints it out along with the tree structure. The balance factor of a node is the height of its left subtree minus the height of its right subtree, and a node with balance factor 1, 0, or -1 is considered balanced. A node with any other balance factor is considered unbalanced and requires rebalancing the tree. The balance factor is either stored directly at each node or computed from the heights of the subtrees.

Example: use the same nodes in the main method and get balance factor of the root node Output: -2

3-check whether a tree is an AVL tree.Output: false

4-implement the insertion of a node with tree rebalancing insertBalneced(). After inserting a node, it is necessary to check each of the node's ancestors for consistency with the rules of AVL. For each node checked, if the balance factor remains -1, 0, or 1 then no rotations are necessary. However, if the balance factor becomes 2 or -2 then the subtree rooted at this node is unbalanced. If insertions are performed serially, after each insertion, at most two tree rotations are needed to restore the entire tree to the rules of AVL.

There are four cases which need to be considered, of which two are symmetric to the other two. Let P be the root of the unbalanced subtree. Let R be the right child of P. Let L be the left child of P.

Right-Right case and Right-Left case: If the balance factor of P is -2, then the right subtree outweighs the left subtree of the given node, and the balance factor of the right child (R) must be checked. If the balance factor of R is -1, a left rotation is needed with P as the root. If the balance factor of R is +1, a double left rotation is needed. The first rotation is a right rotation with R as the root. The second is a left rotation with P as the root.

Left-Left case and Left-Right case: If the balance factor of P is +2, then the left subtree outweighs the right subtree of the given node, and the balance factor of the left child (L) must then checked. If the balance factor of L is +1, a right rotation is needed with P as the root. If the balance factor of L is -1, a double right rotation is needed. The first rotation is a left rotation with L as the root. The second is a right rotation with P as the root.

output: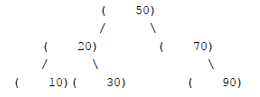

5-implement the deletion of a node with tree rebalancing. The node is a leaf, remove it. If the node is not a leaf, replace it with either the largest in its left subtree (inorder predecessor) or the smallest in its right subtree (inorder successor), and remove that node. The node that was found as replacement has at most one subtree. After deletion, retrace the path back up the tree (parent of the replacement) to the root, adjusting the balance factors as needed.As with all binary trees, a node's in-order successor is the left-most child of its right subtree, and a node's in-order predecessor is the right-most child of its left subtree. In either case, this node will have zero or one children. Delete it according to one of the two simpler cases above.

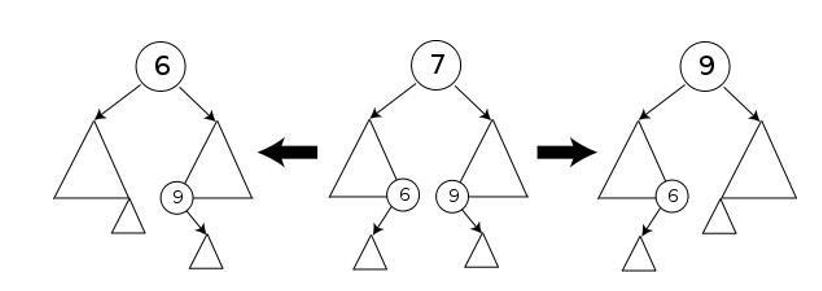
In addition to the balancing described above for insertions, if the balance factor for the tree is 2 and that of the right subtree is 0, a left rotation must be performed on P. The mirror of this case is also necessary.The retracing can stop if the balance factor becomes -1 or 1 indicating that the height of that subtree has remained unchanged. If the balance factor becomes 0 then the height of the subtree has decreased by one and the retracing needs to continue. If the balance factor becomes -2 or 2 then the subtree is unbalanced and needs to be rotated to fix it. If the rotation leaves the subtree's balance factor at 0 then the retracing towards the root must continue since the height of this subtree has decreased by one. This is in contrast to an insertion where a rotation resulting in a balance factor of 0 indicated that the subtree's height has remained unchanged.

This assignment is concerned with AVL trees. Given the code below: return root; import java.util.*; class Node public Node left, right, parent; public int height = 1; //getting the height of the tree private static int TreeHeight (Node N) i public int value; if (N null) return 0; return N.height; public Node (int val) f this.value val; //Balancing the tree private Node insertBalneced (Node node, int value) if (nodenull)t public class AVLTree return (new Node (value)); private Node insertNode (Node root, int key) root - insertRec (root, key) PrintTreestruc- ture (root)System.out.println ) if (value root.value) i root.right - insertRec (root.right, key); root .height = Math.max (TreeHeight (root. Ieft), Height (root.right)) t1; Tree