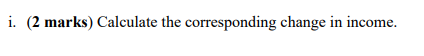
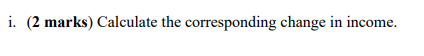
1. (24 marks) Consider the utility function U = min{axy, bx;}. where the price of x, is p,, the price of x; 1s p, and consumer income 15 M. a. (2 marks) Calculate the consumer's optimal bundle. b. (2 marks) Calculate the consumer's indirect utility function (ie, the consumer's maximised utility as a function of p,, p, and m). Assume that the price of x; changes to p;. c. (2 marks) Calculate the consumer's new optimal bundle. d. (2 marks) Calculate the consumer's new indirect utility function (1e, the consumer's new maximised utility as a function of py, p; and m). Assume that the consumer is offered the opportunity to return to the original prices, (py, p2), but offered a corresponding adjustment in their income, m m', so that they can keep their new level of utility. e. (2 marks) State whether this situation 1s referring to compensating or equivalent variation. f. (2 marks) Calculate the corresponding change 1n income. g. (2 marks) Briefly explain whether the answer n part (f) 1s positive or negative. Now assume that the consumer is offered the opportunity to stay at the new prices, (p1, p2), but offered a corresponding adjustment in their income, m m', so that they can keep their original level of utility. h. (2 marks) State whether this situation 1s referring to compensating or equivalent variation. 1. (2 marks) Calculate the corresponding change 1n income. j. (2 marks) Briefly explain whether the answer in part (i) is positive or negative. k. (2 marks) Briefly explain if compensating variation or equivalent variation is bigger (in absolute value terms). 1. (2 marks) Briefly explain how to approximate the change in consumer surplus associated with the change in price when the demand function is non-linear.d. (2 marks) Calculate the consumer's new indirect utility function (1e, the consumer's new maximised utility as a function of py, p; and m). a. To find the consumer's optimal bundle, we need to minimize the utility function U' = min(a*1, b*2) subject to the budget constraint p1a + pab = m. To solve this, we set up the Lagrangian: = min(a*1,b*2) + A(m p1a p2b) Taking the first-order conditions with respect to a and b, we have: o J1-2Ap1=0 (1) Apy =0 (2) da ac {2_)'1'2_0 (3) 8 = T Agi=10 (4) From equations (1) and (3), we get: Therefore, ps = 2p1. Substituting this into the budget constraint: pa+2pb=m a+2b="2 The optimal bundle satisfies a = g andb = 0. b. The indirect utility function is the maximum utility attainable given prices and income. Since b = 0in the optimal bundie: U(p1, po,m) = min (2,0) = = . When the price of x; changes to p'l, the new optimal bundle is obtained by setting the new price in the original utility maximization problem. Since b = 0 and ps = 2p), the new budget constraint becomes: pla=m So the new optimal bundleisa = P\f. To keep the same level of utility, the change in income m' must compensate for the change in price. So: U(plnp?:m) U(pllipzim,) m _ m M 7 Solving for m', we get: f ! B m =_-m n g. The change in income is positive because the consumer needs more income to maintain the same level of utility when facing a higher price for ;. h. This situation refers to compensating variation