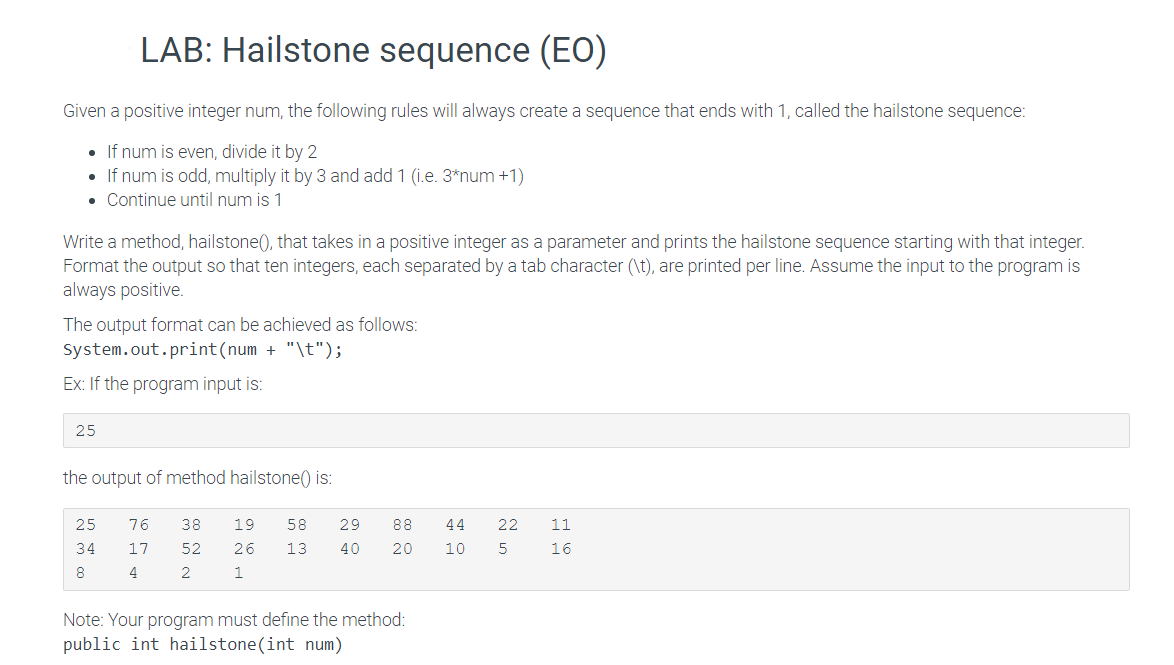
$\mathrm{.}17$ LAB: Hailstone Numbers

Learning objectives

In this lab, you will:

Write a function which reduces a particular number to $1$ using hailstone number sequences

Write a function to compare the number of iterations it takes between two numbers to get to $1$

Motivation

One currently unsolved problem in mathematics looks at sequences of numbers, sometimes called hailstone numbers.

Given a positive integer n$,$ the following rules will always create a sequence that ends with $1,($called the hailstone sequence$)$:

If n is even, divide it by $2$

If n is odd, multiply it by $3$ and add $1($i$.$e$.3$n $+1)$

Continue until n is $1$

From any starting number, you can make a sequence of numbers, applying this rule repeatedly.

Mathematicians guess that if you apply the rule enough times to any natural number, you'll eventually end up with $1($which then is tripled plus one to get $4,$ then $2,$ then $1$ again in an endless cycle$).$ The formalization of this guess is called the Collatz Conjecture, and it is one of the most well$-$known open $($i$.$e$.,$ unsolved$)$ problems in mathematics.

Instructions:

Feel free to write your own assert statements to test and debug your functions.

Part $1$: Generate a hailstone sequence

Write a function get$\_$hailstone$\_$seq$()$ that takes an integer and returns a list that contains hailstone numbers $($as integers$)$ starting from that integer and up until the first digit $1.$

assert get$\_$hailstone$\_$seq$(8)==[8,4,2,1]$

assert get$\_$hailstone$\_$seq$(5)==[5,16,8,4,2,1]$

Part $2$: Get the shorter hailstone sequence

Write a function shorter$\_$hailstone$\_$seq$()$ that takes two integers and returns a list that contains the shorter hailstone sequence. If the sequences have the same length, return the one that corresponds to the first parameter. The function calls the get$\_$hailstone$\_$seq$()$ as its helper function.

assert shorter$\_$hailstone$\_$seq$(5,8)==[8,4,2,1]$

assert shorter$\_$hailstone$\_$seq$(5,7)==[5,16,8,4,2,1]$

Deconstructing an example

Let's look at shorter$\_$hailstone$\_$seq$(10,21).$ In this case, num$1$ is $10$ and num$2$ is $21.$

First, let's look at num$1$:

since $10$ is even, we can get the next number by dividing it by $2,$ so $10/2=5$

since $5$ is odd, the next number is $5*3+1=16$

then $16/2=8,$

then $8/2=4,$

then $4/2=2,$

then $2/2=1,$ and we've arrived at $1$ in $6$ steps.

The resulting sequence is $[10,5,16,8,4,2,1].$

Then, let's look at num$2$:

since $21$ is odd, the next number is $21*3+1=64$

since $64$ is even, the next number is $64/2=32$

then $32/2=16,$

then $16/2=8,$

then $8/2=4,$

then $4/2=2,$

then $2/2=1,$ and we've arrived at $1$ in $7$ steps.

The resulting sequence is $[21,64,32,16,8,4,2,1].$

So since $6$ is strictly fewer than $7$ steps, our function returns the sequence that corresponds to the number $10,$ i$.$e$.,[10,5,16,8,4,2,1].$

assert shorter$\_$hailstone$\_$seq$(10,21)==[10,5,16,8,4,2,1]$