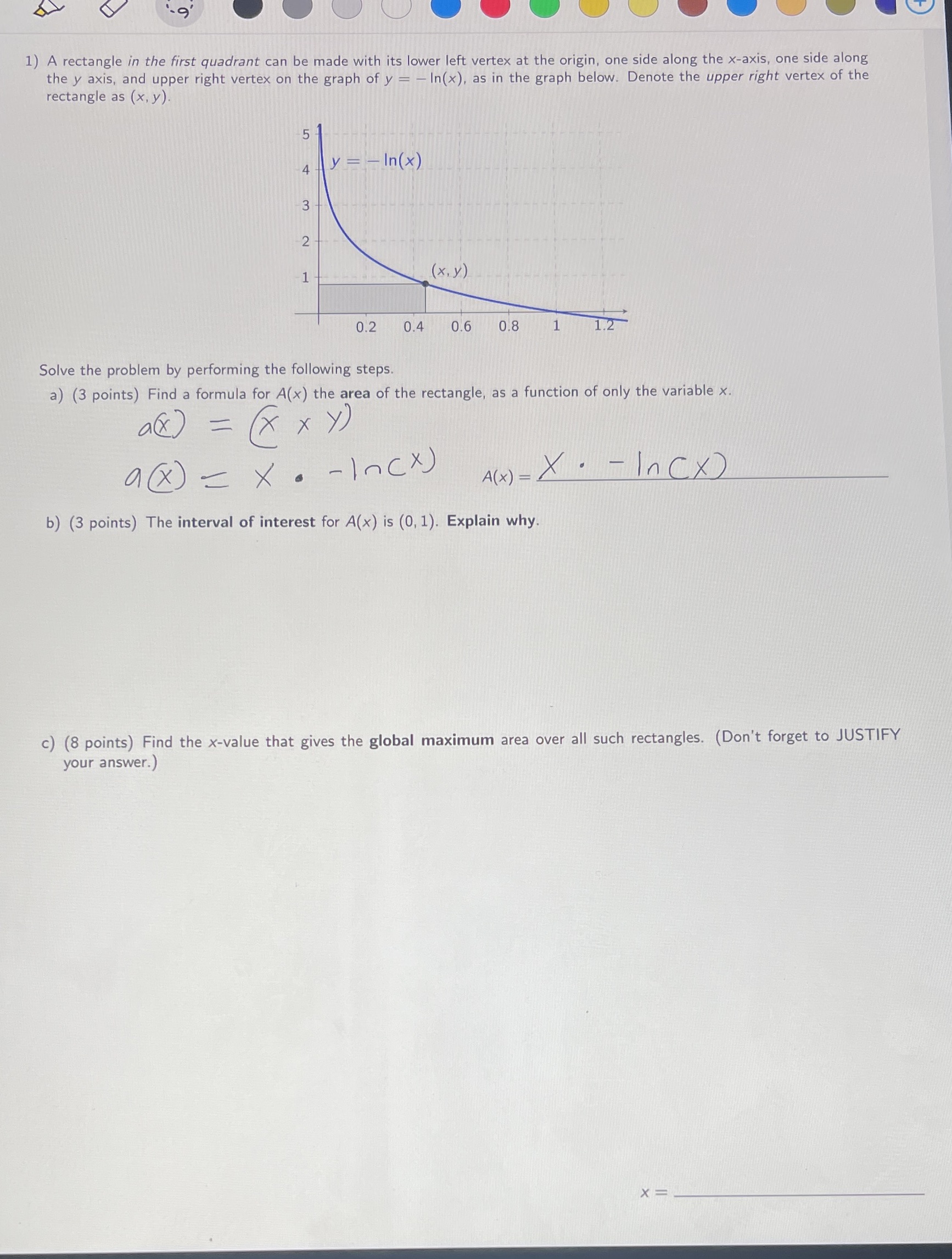
1- 9' 1) A rectangle in the first quadrant can be made with its lower left vertex at the origin, one side along the x-axis, one side along the y axis, and upper right vertex on the graph of y = - In(x), as in the graph below. Denote the upper right vertex of the rectangle as (x, y). 4 - In (x ) 3 2 1 ( x, y ) 0.2 0.4 0.6 0.8 1 1.2 Solve the problem by performing the following steps. a) (3 points) Find a formula for A(x) the area of the rectangle, as a function of only the variable x. al ) = ( x x y ) a ( x ) = x . - Inc x ) A ( x ) = X . - Inc x ) b) (3 points) The interval of interest for A(x) is (0, 1). Explain why. c) (8 points) Find the x-value that gives the global maximum area over all such rectangles. (Don't forget to JUSTIFY your answer.)