1

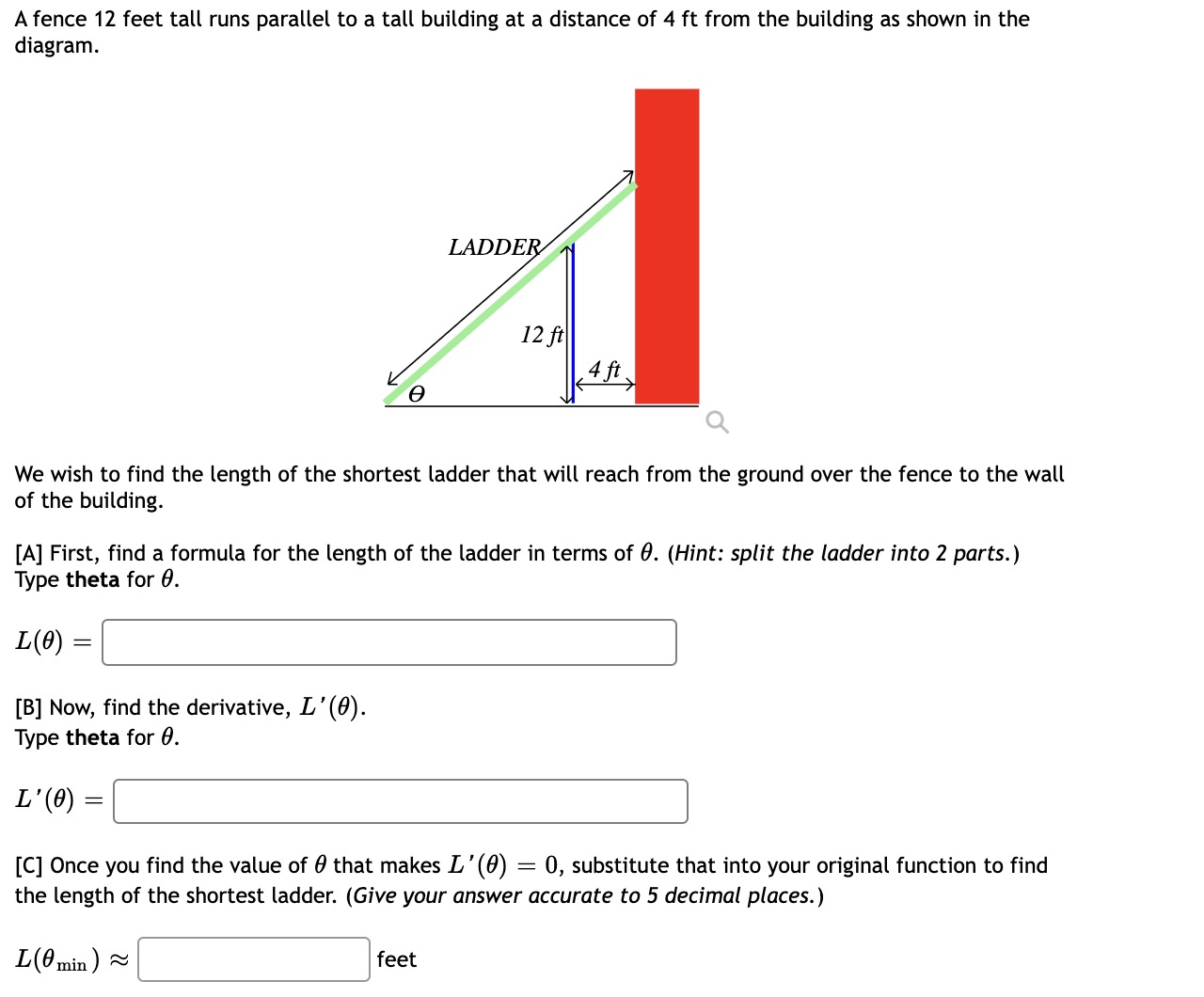
A box with a square base and open top must have a volume of 108000 cm\". We wish to find the dimensions of the box that minimize the amount of material used. First, find a formula for the surface area of the box in terms of only as, the length of one side of the square base. [Hintz use the volume formula to express the height of the box in terms of 35.] Simplify your formula as much as possible. Me) = Next, find the derivative, A '(m). Now, calculate when the derivative equals zero, that is, when A'(a:) = 0. [Hintz multiply both sides by 9:2 -] We next have to make sure that this value of :1: gives a minimum value for the surface area. Let's use the second derivative test. Find A"(:c). mm = Evaluate A"(a:) at the x-value you gave above. NOTE: Since your last answer is positive, this means that the graph of A(a:) is concave up around that value, so the zero of A '(m) must indicate a local minimum for A(a:). (Your boss is happy now.) For the given cost function C(m) = 62500 + 4003 + m2 find: a) The cost at the production level 1900 b) The average cost at the production level 1900 c) The marginal cost at the production level 1900 d) The production level that will minimize the average cost e) The minimal average cost For the given cost function C(w) = 10000 + 400.1: + .172, First, find the average cost function. Use it to find: a) The production level that will minimize the average cost in) The minimal average cost 5:] If 2100 square centimeters of material is available to make a box with a square base and an open top, find the largest possible volume of the box. A fence 12 feet tall runs parallel to a tall building at a distance of 4 ft from the building as shown in the diagram. LADDE 12f: 4ft 9 q We wish to find the length of the shortest ladder that will reach from the ground over the fence to the wall of the building. [A] First, find a formula for the length of the ladder in terms of 0. (Hint: split the ladder into 2 parts.) Type theta for 6. 15(9):: [B] Now, find the derivative, L'(9). Type theta for 6. m) [C] Once you find the value of 6 that makes L '(6) = 0, substitute that into your original function to find the length of the shortest ladder. (Give your answer accurate to 5 decimal places.) m...) W