Question: 1. (a) Use the Euclidean algorithm to find d = god(2022, 1021). (b) Find integers x, y such that 2022x + 1021y = d. (c)

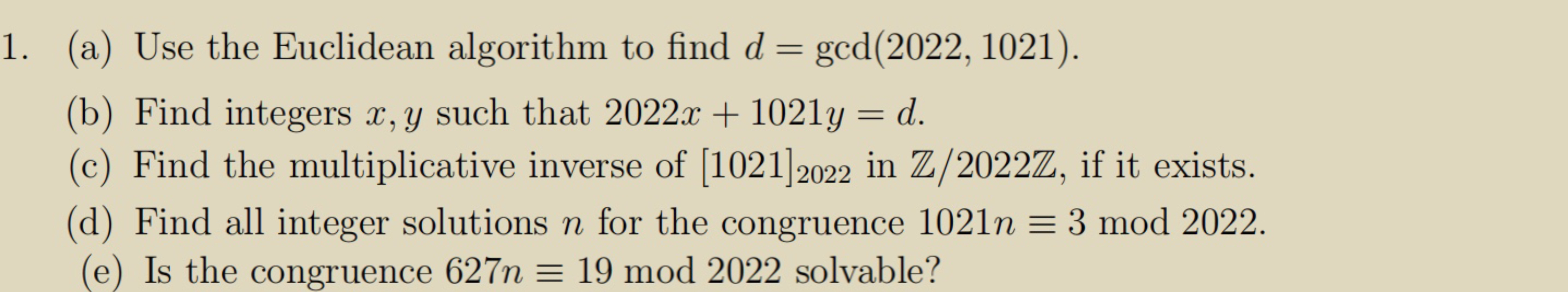
1. (a) Use the Euclidean algorithm to find d = god(2022, 1021). (b) Find integers x, y such that 2022x + 1021y = d. (c) Find the multiplicative inverse of [1021]2022 in Z/2022Z, if it exists. (d) Find all integer solutions n for the congruence 1021n = 3 mod 2022. (e) Is the congruence 627n = 19 mod 2022 solvable

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

1. (a) Use the Euclidean Algorithm to find the inverse of 41 in Z131. (b) Use (a) to solve the equation 41x + 1 = 10 in Z131. 2. Using Fermat's Little Theorem, find the remainder when 31403 is...

1. Find an inverse of a modulo m for each of these pairs of relatively prime integers using the method followed in example below. a.) a = 4 , m = 9 b) a =19, m = 141 c) a = 55, m = 89 d) a = 89, m =...

This is Discrete Mathematics, Any help would be greatly appreciated. Thanks! 1. Let n be a positive integer. The relation congruence modulo n on the set Z is de?ned by: for all x, y ?Z, x ? y (mod n)...

6. Let a=315,b=825. (a) Use the Euclidean algorithm to find the greatest common divisor of the pair of integers a, b. (5 points) To find the greatest common divisor (god) of a=315 and b=825 using the...

1. Describe how to construct a field of order 8 = 23 as a quotient ring R/I (i.e., state what the appropriate ring R and ideal I are). In particular, describe what the elements of the ring R/I are...

help me to solv this please Homework 1. What are the quotient and remainder when: -123 is divided by 19? 2. Find a divm and a mod when a=-10101,w=333. 3. Find the value of [(-133 mod 23 +261 mod 23)...

please all questions ! Specifications - Written Assignment must be readable. - Any assignment will be due on the date of next week - Late Submission criteria is set to deduct 10% per day for late...

3. [10 marks total] (a) [4 marks] Use the Euclidean Algorithm to find god(129, 889). (b) [4 marks] Use the twopass Euclidean Algorithm method to express the god(129, 889) as a linear combination of...

Math 311W: Discrete Math Homework 5, due on Friday, Feb. 17 Note: Whenever applicable, please give your final answers using the standard representatives, i.e., in the form [a]n where 0 6 a

Find the prime factorization of each of these integers. a) 97 b) 81 c) 24 d) 143 e) 169 f) 625 Use the Euclidean algorithm to find a) gcd(45, 30). b) gcd(301, 300). c) gcd(277, 123). d) gcd(180, 42)....

The horizontal axis is labeled quantity. The vertical axis is labeled price. A rising curve labeled S and a falling curve labeled D are plotted. The point of intersection of the S and D curves...

Burns Company incurred the following costs during the year: direct materials $24.50 per unit; direct labor $15.60 per unit; variable manufacturing overhead $18.10 per unit; variable selling and...

Which of the following statements is true regarding using quantitative measures to conduct risk analysis? The correlation of corporate risk and market risk should override any qualitative factors...

Rinad the rogutements Requirements 1. Pepare the journal entiles for Harnithen Conpany for the sele of the merchandive, the cost of the salk, and the related teceipt st payme nt from payment is...