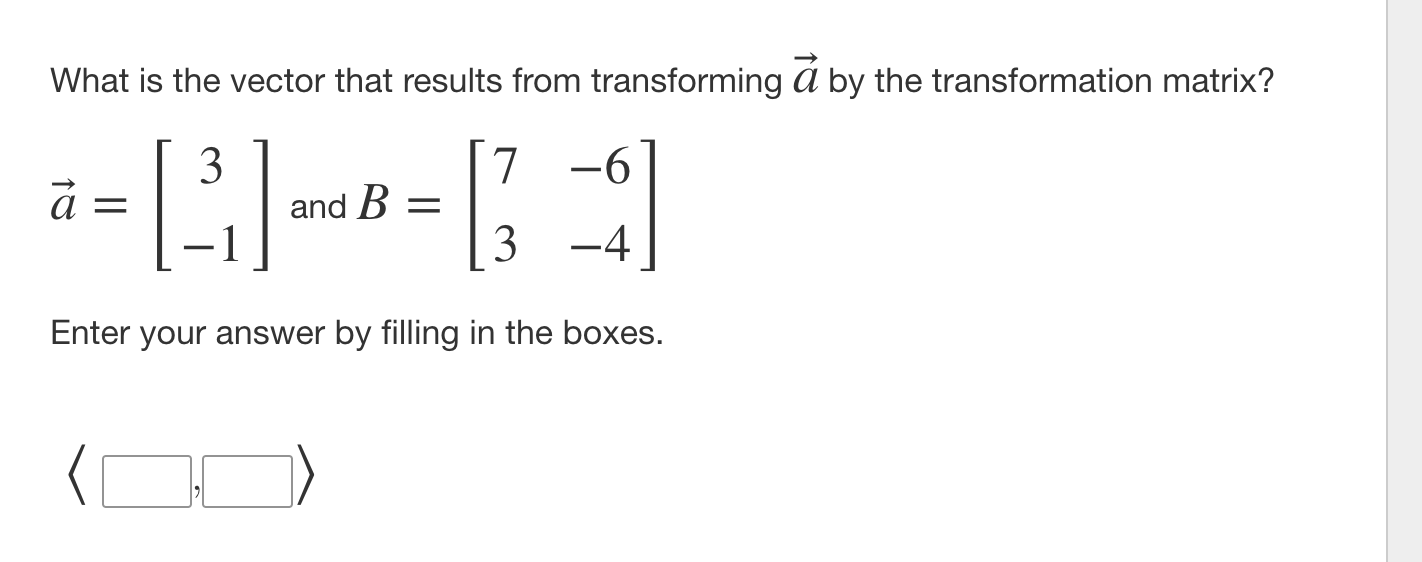
1. a=2,1 and b=1,3.

Represent a+b by using the parallelogram method.

Use the Vector tool to draw the vectors, complete the parallelogram method, and draw a+b.

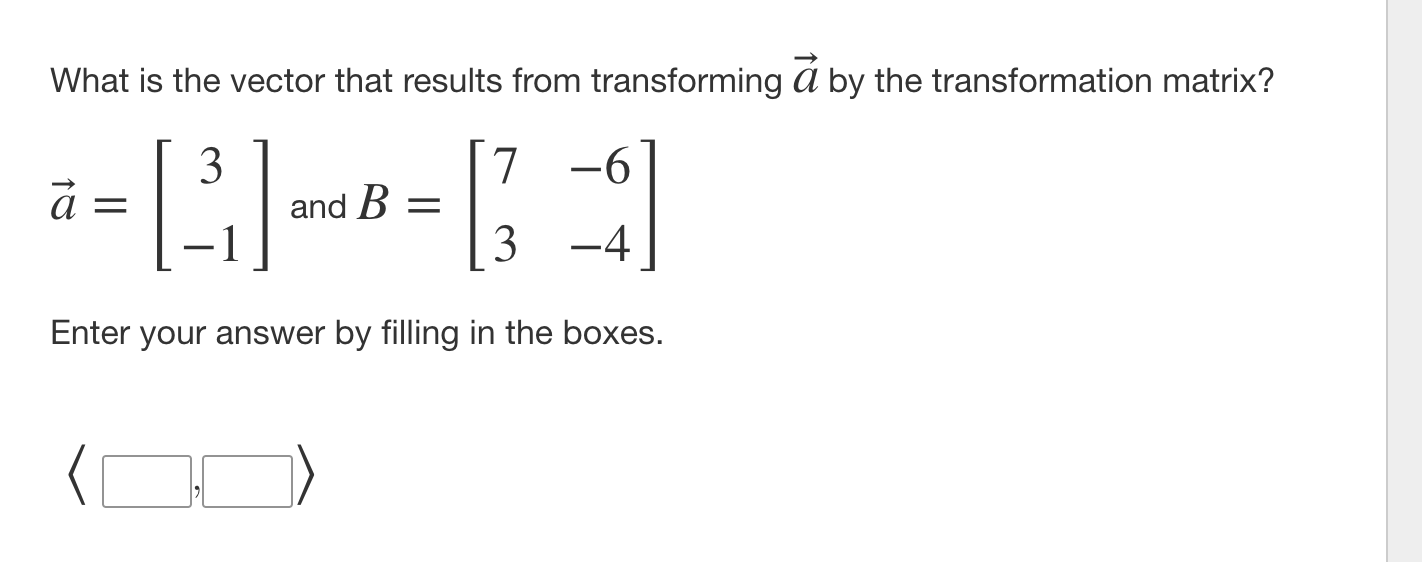
21' = (5, 1>andb = (3, 4). Represent a + b by using the head to tail method. ) Use the Vector tool to draw the vectors, complete the head to tail method, and draw 21' + b. Do not draw any unnecessary vectors. To use the Vector tool, select the initial point and then the terminal point. Vector 6 Undo I" Redo x Reset 'y a = (2, - 1) and b = (1, 3). Represent a + b by using the parallelogram method. Use the Vector tool to draw the vectors, complete the parallelogram method, and draw a + b. To use the Vector tool, select the initial point and then the terminal point. + Move Vector Undo Redo x Reset y 7 6 5 3 2 1 X -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 -2 -3 -49 What is the component form of resultant of 2b 3a? a = (2, 3) 25 (-15) Enter your answer by filling in the boxes. 25 32%: (3,3) What is the vector that results from transforming Q by the transformation matrix? 3 7 -6 a and B = 3 -4 Enter your answer by filling in the boxes.What is the component form of the vector whose tail is the point (3, 2) and whose head is the point (1, 6)? (S:D> A ship leaves port at noon and travels at a bearing of 214. The ship's average rate of speed is 15 miles per hour. Describe the location of the ship at 2:30 p.m. by writing a vector in component form. Then explain what these components mean in terms of the scenario. Drag a value into each box to correctly complete the statements. The component form of the vector representing the ship at 2:30 p.m. is approximately . This means that the ship is about miles to the and about miles to the of where the ship left port. -31 -21 -12.4 -8.4 8.4 12.4 21 31 north south east west