1. As the standard deviation for Martin Products' distribution increases, the distribution for Martin Products:

a. becomes steeper and more like the distribution for U.S. Water

b. does not change

c. becomes flatter and less like the distribution for U.S. Water

d. might either become steeper or flatter

2. Use the slider to set the standard deviation for Martin Products to be 6.0. The probability of having a rate of return of at least 5% (move the cursor to 5.0)

a.is greater for U.S. Water than for Martin Products

b.is the same for both U.S. Water and the Martin Products distribution

c.is greater for Martin Products than U.S. Water

d. cannot be determined

3. Use the slider to set the standard deviation for the Martin Products distribution to 8.0. The probability of having a rate of return of at least 10% (move the vertical line to 10.0)

a. is greater for U.S. Water than for Martin Products

b. is the same for both U.S. Water and the Martin Products distribution

c. is greater for Martin Products than U.S. Water

d. cannot be determined

4. Suppose the standard deviation for the Martin Products Distribution is 4.0. If an investor is hoping for a return of at least 13%, the chances that investing in Martin Products will return at least 13%

a. are much less than in investing in U.S. Water

b. are the same as investing in U.S. Water

c. are greater than in investing in U.S. Water

d. cannot be determined

5. As the standard deviation of outcomes for Martin Products increases, investing in Martin Products becomes riskier because

a. the range of outcomes having some probability becomes wider

b. an outcome at or near the expected return of 10% becomes less likely

c. although the chances of some big gains increase, the chances for some big losses also increase.

d. all of the above reasons

e. none of these

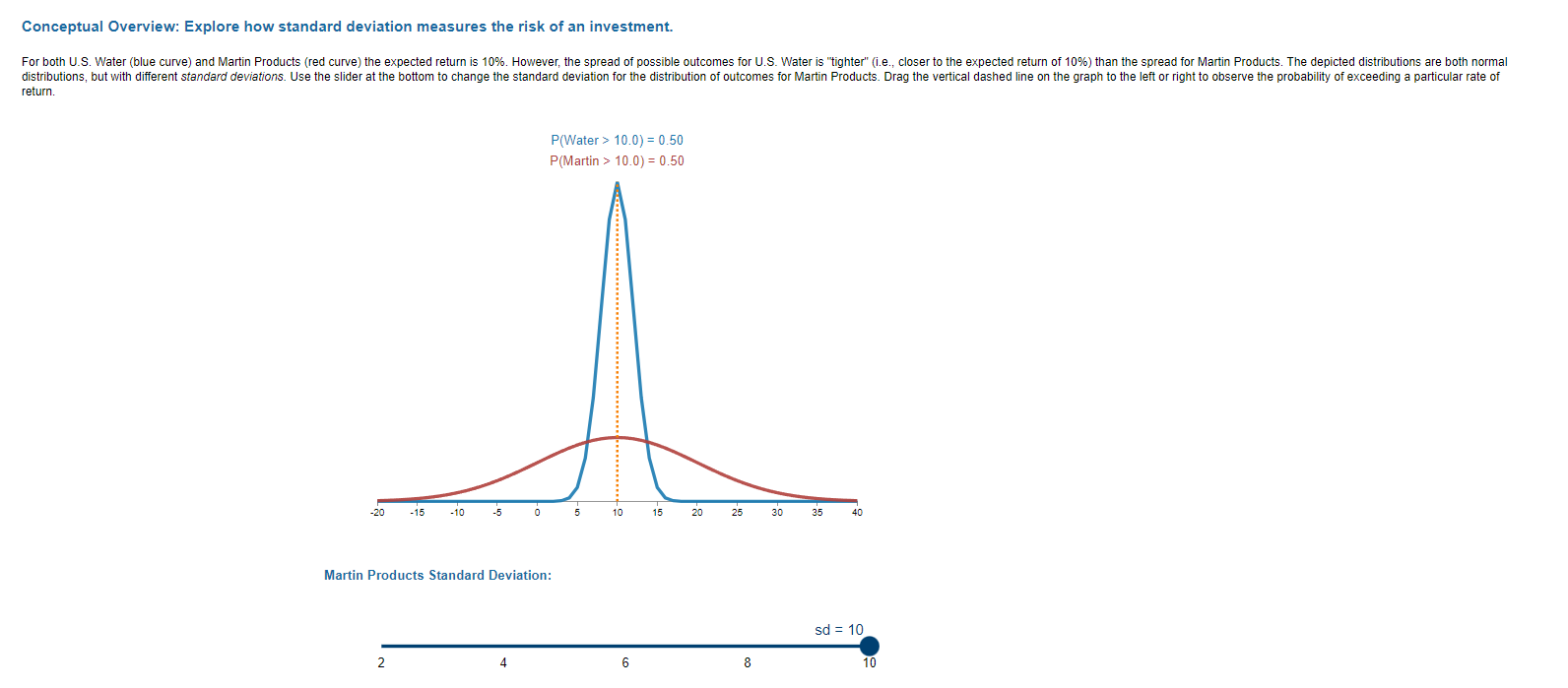
Conceptual Overview: Explore how standard deviation measures the risk of an investment. return. P(Water>10.0)=0.50P(Martin>10n)=05n Martin Products Standard Deviation: Conceptual Overview: Explore how standard deviation measures the risk of an investment. return. P(Water>10.0)=0.50P(Martin>10n)=05n Martin Products Standard Deviation