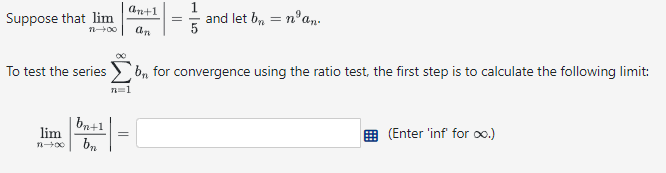
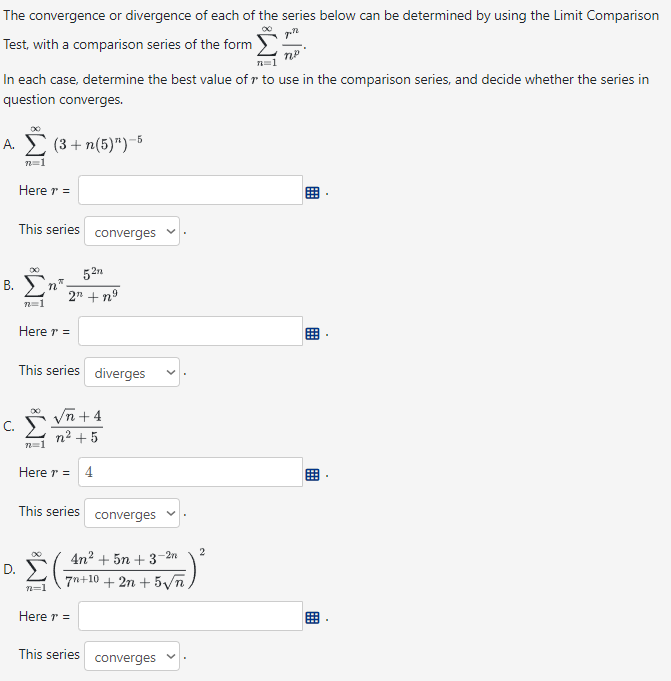
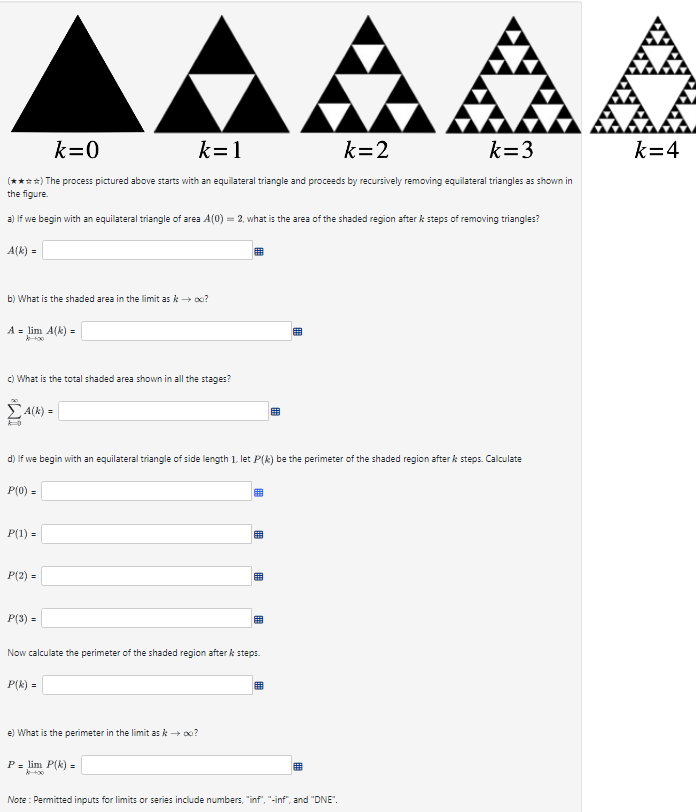
1 Cn 1 = and let b,, = na,,. Suppose that lim Ti 0o - To test the series Z by, for convergence using the ratio test, the first step is to calculate the following limit: n=1 = B (Enter inf for cc.) The convergence or divergence of each of the series below can be determined by using the Limit Compariscn s k[ , . : T Test, with a comparison series of the form E T n=1 In each case, determine the best value of r to use in the comparison series, and decide whether the series in guestion converges. K A Y (B+n(s)) " n=1 Here 7 = B - This series converges v - el 5'311 w B. Z, gn | pl n=]1 Here r = . This series diverges v - $ e 2 E - n + 3 Herer= 4 = - This series converges ~ - - = ( 4n* + 5n4 372 )2 C A\\ 0 L9 4 By Here r = H . This series converges ~ - KAZAA k=0 k=1 k=2 k=3 k=4 (* *# #) The process pictured above starts with an equilateral triangle and proceeds by recursively removing equilateral triangles as shown in the figure. a) If we begin with an equilateral triangle of area A(0) = 2, what is the area of the shaded region after k steps of removing triangles? A(k) = by What is the shaded area in the limit as * -> Do? A = lim A(k) = c) What is the total shaded area shown in all the stages? SA(K) = d) If we begin with an equilateral triangle of side length 1, let P() be the perimeter of the shaded region after k steps. Calculate P(0) = P(1) = P(2) = P(3) = Now calculate the perimeter of the shaded region after k steps. P(k) = e) What is the perimeter in the limit as * -> Do? P = lim P(k) = Note : Permitted inputs for limits or series include numbers, "inf", "-inf", and "DNE&quot