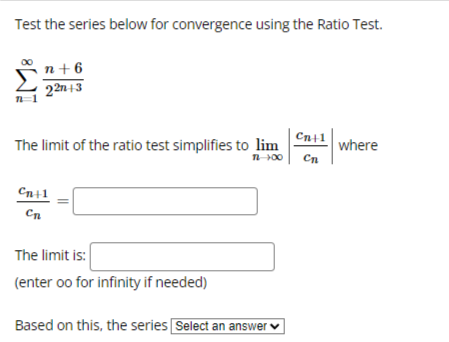
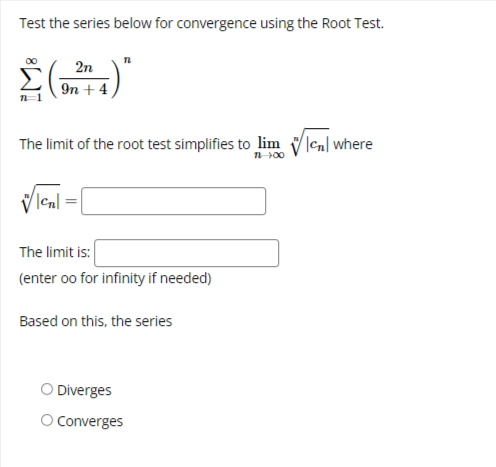
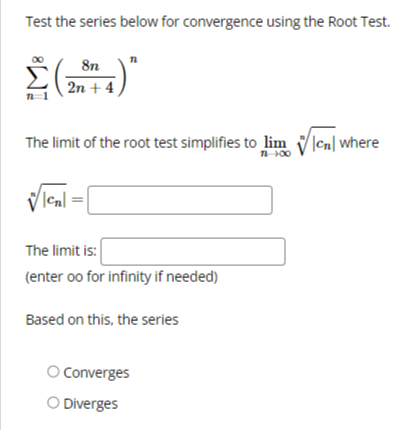
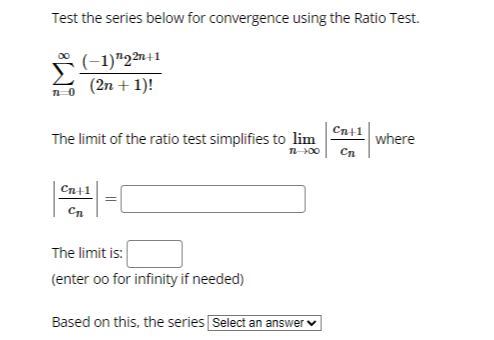
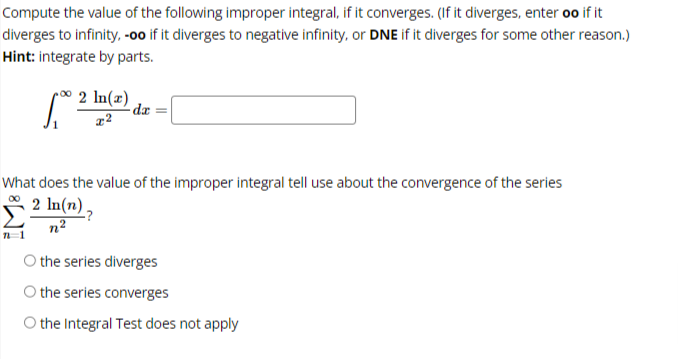
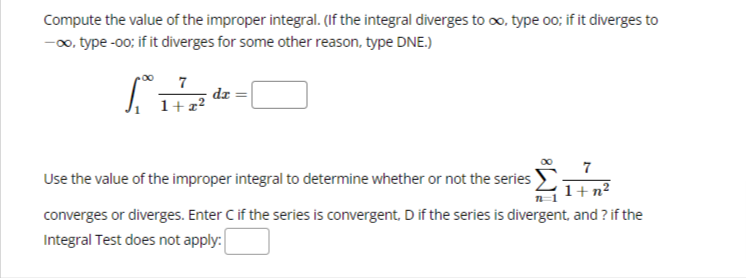
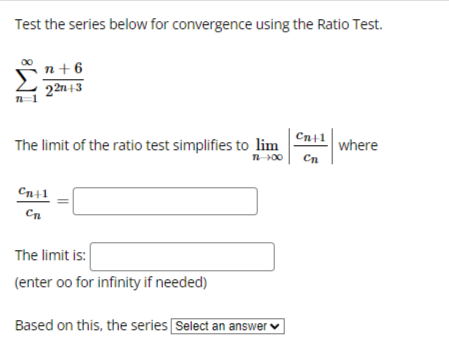
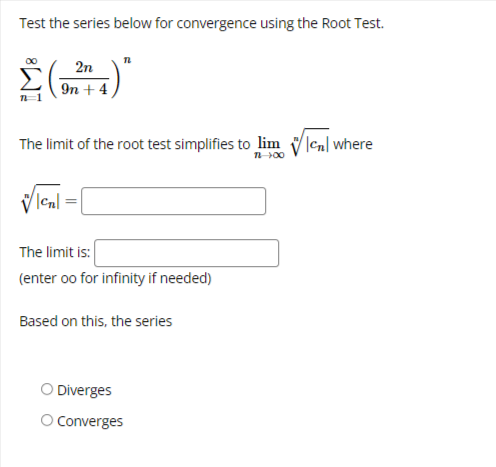
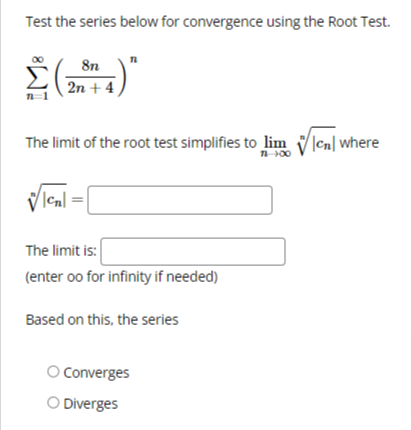
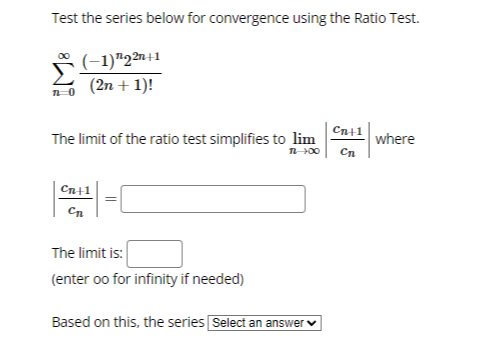
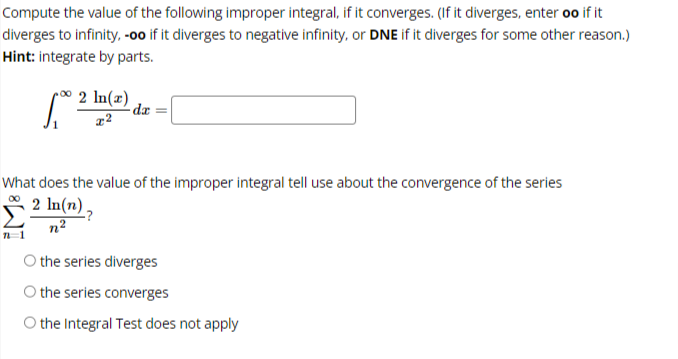
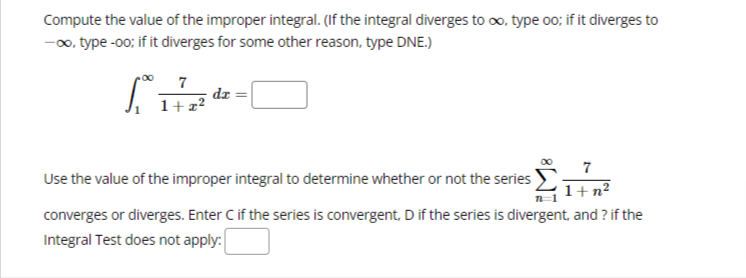
We want to use the Comparison Test to determine if the series: k 1 k4 - 15 converges or diverges by comparing it with: 1 We can conclude that: O The first series diverges by comparison with the second series. O The first series converges by comparison with the second series. O The Comparison Test is inconclusive in this situation.Test the series below for convergence using the Ratio Test. n +6 22n43 n 1 The limit of the ratio test simplifies to lim where Cn Cn The limit is: (enter oo for infinity if needed) Based on this, the series Select an answer vTest the series below for convergence using the Root Test. 2n M 9n + 4 The limit of the root test simplifies to lim V Ical where 1 100 VIcal The limit is: (enter oo for infinity if needed) Based on this, the series O Diverges O ConvergesTest the series below for convergence using the Root Test. 00 8n n n 1 2n + 4 The limit of the root test simplifies to lim v |ca| where n-100 VIcal = The limit is: (enter oo for infinity if needed) Based on this, the series O Converges O DivergesTest the series below for convergence using the Ratio Test. DO (-1)2 2n +1 n-0 (2n + 1)! Cn41 The limit of the ratio test simplifies to lim where Cn Cn41 Cn The limit is: (enter oo for infinity if needed) Based on this, the series Select an answer vCompute the value of the following improper integral, if it converges. (If it diverges, enter oo if it diverges to infinity, -oo if it diverges to negative infinity, or DNE if it diverges for some other reason.) Hint: integrate by parts. 2 In(I) de = What does the value of the improper integral tell use about the convergence of the series 2 In(n) -? n2 n 1 O the series diverges O the series converges O the Integral Test does not applyCDmpUtE the value of the improper integral. {If the integral diverges to no. type oo; if the integral diverges to oo. type oo; and if the integral diverges for some other reason, type DNE.J f: [:3}. =:J m 1 Use your answer to help determine whether the series 2 converges or diverges. Enter a 2 [4" _ 3)? C if the series is convergent. D if the series is divergent. or ? if the Integral Test does not apply: Ll liCornptrte the value of the improper integral. {If the integral diverges to oo. type oo: if it diverges to oIo. type oo; if it diverges for some other reason. type ONE} '3\" r f, 1+.2~e=l:] on 1' Use the value of the improper integral to determine whether or not the series 2 l + 2 n 1 - converges or diverges. Enter C if the series is convergent. D ifthe series is divergent and .7 if the Integral Test does not apply