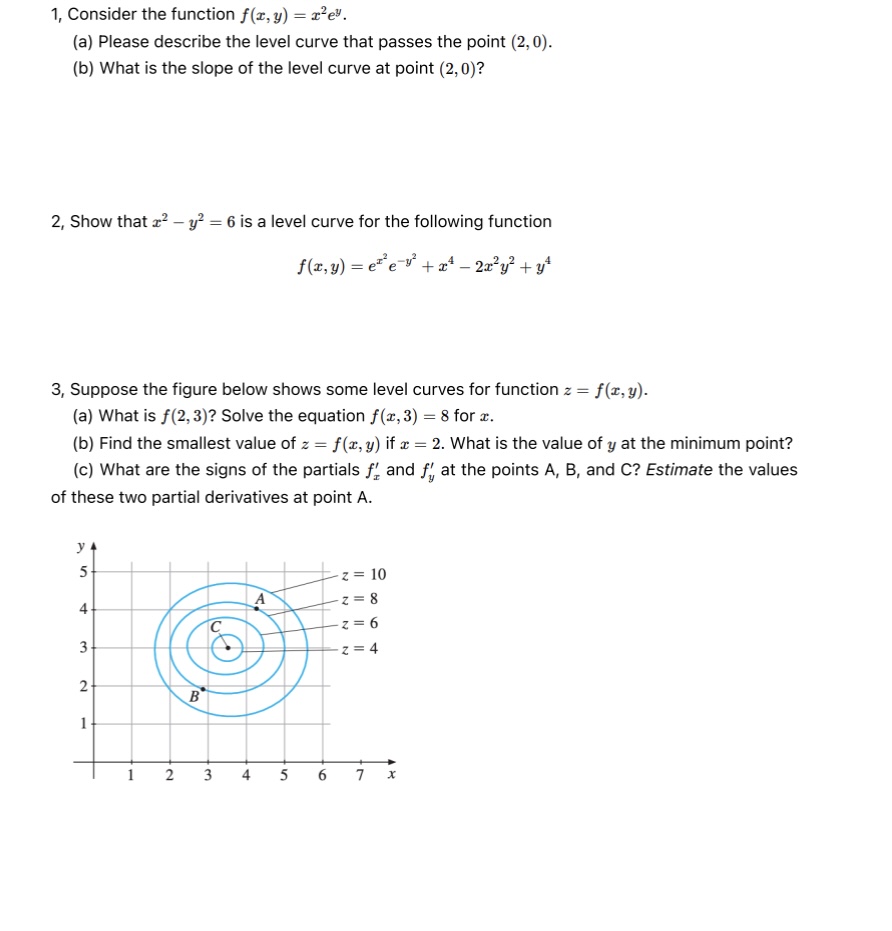
1, Consider the function f(z,y) = z'e. (a) Please describe the level curve that passes the point (2,0). (b) What is the slope of the level curve at point (2,0)? 2, Show that z* y* = 6 is a level curve for the following function flz,y) = .3'26'3"2 S 2:2y2 + y'i 3, Suppose the figure below shows some level curves for function z = f(z,y). (a) What is f(2, 3)? Solve the equation f(z,3) = 8 for z. (b) Find the smallest value of z = f(z,y) if = 2. What is the value of y at the minimum point? (c) What are the signs of the partials f; and , at the points A, B, and C? Estimate the values of these two partial derivatives at point A. 4, Examine the convexity/concavity of the function f(z,y) = Inz + y e**. 5, The equation 3z 3zy\" + 3y' + 3y* = 4 defines y implicitly as function h(z) of x in a neighborhood of the point (1,1). Find the derivative h'(1). G, Let D(p,q) and E(p,q) be the demands for two commodities when the prices per unit are p and g, respectively. Suppose the commodities are substitutes in consumption, such as butter and margarine. What are the normal signs of the partial derivatives of D and E with respect to p and ? Explain. 7, Suppose the production function is Q(K,L) = 100K%*L"7. Let M Px denotes the marginal product of capital, M P, denotes the marginal product of labor. (a) Is M Px a function of K alone, or both K and L? What about M P.? (b) Find the slope of the isoquant at point (K, L) = (50, 10); also, find the gradient vector at this point. (please round your answer to two decimal places) 8, Consider the function f defined for all (x,y) such that f(z,y) = 2 + y* 6z + 8y + 35. (a) This function has a minimum point. Find it. (b) Show that f(x,y) can be written as f(z,y) = (z 3)> + (y +4)? + 10. Explain why this shows that you have really found the minimum in part (a). 9, (bonus points) Suppose that a monopolist firm faces two inverse demand functions P, =200 - 2Q, and P, = 180 4@),, and that the cost function is C = 20(Q, + Q). (a) How much should be sold in the two markets to maximize total profit? What are the corresponding prices? (b) How much profit will be lost if it becomes illegal to discriminate